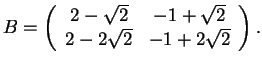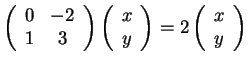 .
Το παραπάνω σύστημα έχει μια ελεύθερη μεταβλητή και εύκολα
βλέπουμε ότι το
.
Το παραπάνω σύστημα έχει μια ελεύθερη μεταβλητή και εύκολα
βλέπουμε ότι το 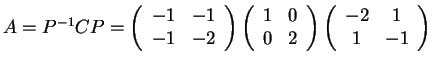 .
Eύκολα βλέπει κανείς χρησιμοποιώντας επαγωγή
ότι
.
Eύκολα βλέπει κανείς χρησιμοποιώντας επαγωγή
ότι
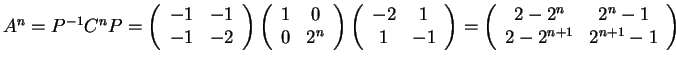 για κάθε
για κάθε
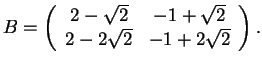
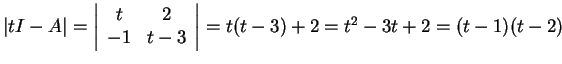 και
άρα από γνωστό θεώρημα ο
και
άρα από γνωστό θεώρημα ο 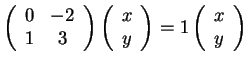 .
Το παραπάνω σύστημα έχει μια ελεύθερη μεταβλητή και άρα το
.
Το παραπάνω σύστημα έχει μια ελεύθερη μεταβλητή και άρα το
Όμοια για την ιδιοτιμή ![]() έχω
έχω
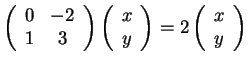 .
Το παραπάνω σύστημα έχει μια ελεύθερη μεταβλητή και εύκολα
βλέπουμε ότι το
.
Το παραπάνω σύστημα έχει μια ελεύθερη μεταβλητή και εύκολα
βλέπουμε ότι το ![]() είναι μια βάση του ιδιοχώρου
που αντιστοιχεί στην ιδιοτιμή 2. Έτσι
είναι μια βάση του ιδιοχώρου
που αντιστοιχεί στην ιδιοτιμή 2. Έτσι
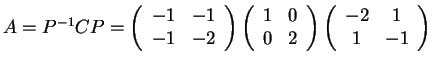 .
Eύκολα βλέπει κανείς χρησιμοποιώντας επαγωγή
ότι
.
Eύκολα βλέπει κανείς χρησιμοποιώντας επαγωγή
ότι
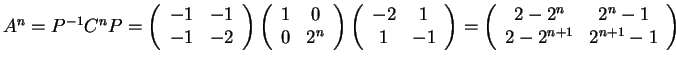 για κάθε
για κάθε
![]() .
Αντικαθιστώντας το
.
Αντικαθιστώντας το
![]() με
με ![]() παίρνω
παίρνω