


Next: Άσκηση 18
Up: Άσκηση 17
Previous: Υπόδειξη
Eφόσον ο  είναι διαγωνοποιήσιμος υπάρχει πίνακας
είναι διαγωνοποιήσιμος υπάρχει πίνακας 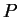 τέτοιος
ώστε
τέτοιος
ώστε 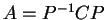 όπου ο
όπου ο 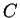 είναι ένας διαγώνιος πίνακας με
στοιχεία στην κύρια διαγώνιο τις ιδιοτιμές του
είναι ένας διαγώνιος πίνακας με
στοιχεία στην κύρια διαγώνιο τις ιδιοτιμές του  ,
δηλαδή
,
δηλαδή
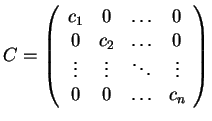 όπου τα
όπου τα 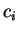 είναι οι ιδιοτιμές του
είναι οι ιδιοτιμές του  οι οποίες είναι
πραγματικοί αριθμοί. Επομένως κάθε
οι οποίες είναι
πραγματικοί αριθμοί. Επομένως κάθε 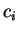 είναι πραγματικός
αριθμός και άρα έχει μια κυβική ρίζα. Αν θέσουμε
είναι πραγματικός
αριθμός και άρα έχει μια κυβική ρίζα. Αν θέσουμε
![$d_i=\sqrt[3]{c_i}$](img202.gif) για κάθε
για κάθε 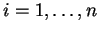 τότε ο πίνακας
τότε ο πίνακας
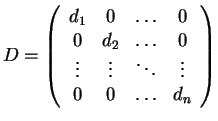 ικανοποιεί την
ικανοποιεί την 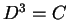 .
Θέτουμε
.
Θέτουμε 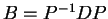 .
Τότε,
.
Τότε,
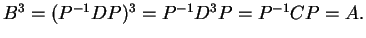
Vassilis Metaftsis
1999-09-15
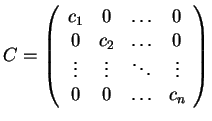 όπου τα
όπου τα 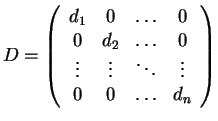 ικανοποιεί την
ικανοποιεί την