


Next: Τριγωνοποίηση
Up: Άσκηση 19
Previous: Υπόδειξη
To χαρακτηριστικό πολυώνυμο του  είναι το
είναι το
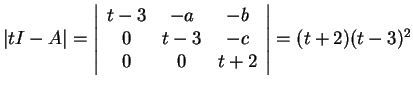 .
Για να είναι ο
.
Για να είναι ο  διαγωνοποιήσιμος θα πρέπει το ελάχιστο πολυώνυμο
του να γράφετε σαν γινόμενο διακεκριμένων πρωτοβάθμιων παραγόντων,
δηλαδή
διαγωνοποιήσιμος θα πρέπει το ελάχιστο πολυώνυμο
του να γράφετε σαν γινόμενο διακεκριμένων πρωτοβάθμιων παραγόντων,
δηλαδή 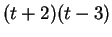 .
Όμως σύμφωνα με το Θεώρημα Cayley - Hamilton
πρέπει
.
Όμως σύμφωνα με το Θεώρημα Cayley - Hamilton
πρέπει
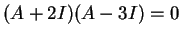 .
Πιο συγκεκριμένα,
.
Πιο συγκεκριμένα,
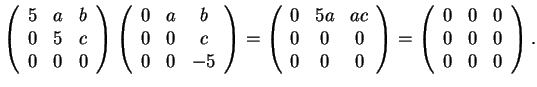 Eπομένως,
Eπομένως, 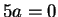 και
και 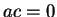 .
Άρα
.
Άρα 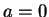 είναι η ζητούμενη συνθήκη.
είναι η ζητούμενη συνθήκη.
Vassilis Metaftsis
1999-09-15
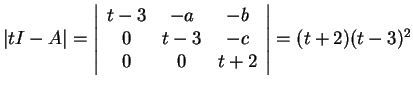 .
Για να είναι ο
.
Για να είναι ο 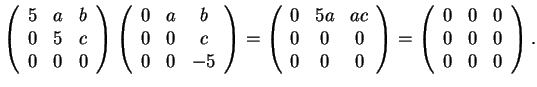 Eπομένως,
Eπομένως,