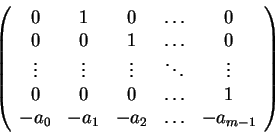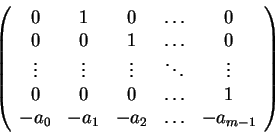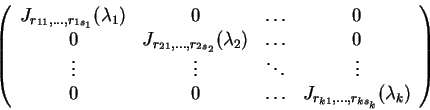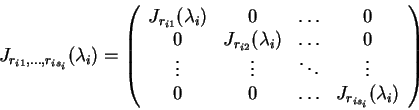Στοιχεία Θεωρίας

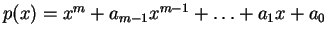
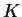
Ορισμός 8   Έστω $p(x)=x^m+a_{m-1}x^{m-1}+\ldots +a_1x+a_0$ ένα πολυώνυμο με συντελεστές στο σώμα $K$. Ο πίνακας

$$\left(\begin{array}{ccccc} 0 & 1 & 0 & \ldots & 0\\ 0 & 0 & ... ... 1\\ -a_0 & -a_1 & -a_2 & \ldots & -a_{m-1} \end{array}\right)$$

λέγεται συνοδός πίνακας του πολυωνύμου $p(x)$.

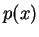
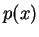
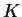
Θεώρημα 15   O συνοδός πίνακας ενός πολυωνύμου $p(x)$ με συντελεστές στο σώμα $K$ και πρώτο συντελεστή την μονάδα έχει ως ελάχιστο και χαρακτηριστικό πολυώνυμο το $p(x)$.

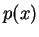
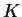
Θεώρημα 16   Ένας πίνακας $A$ με στοιχεία από το σώμα $K$ είναι όμοιος με ένα πίνακα της μορφής

$$\left(\begin{array}{cccc} A_1 & 0 & \ldots & 0\\ 0 & A_2 & \... ...ts & \ddots & \vdots\\ 0 & 0 & \ldots & Α_m \end{array}\right)$$

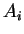
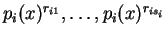
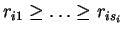
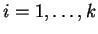
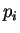
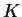
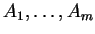
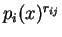
όπου $A_i$ είναι οι συνοδοί πίνακες των πολυωνύμων $p_i(x)^{r_{i1}}, \ldots, p_i(x)^{r_{is_i}}$, $r_{i1}\ge \ldots \ge r_{is_i}$, $i=1,\ldots ,k$. Tα πολυώνυμα $p_i$ είναι διακεκριμένα και ανάγωγα στο $K$ και ο πίνακας είναι μονοσήμαντα ορισμένος εκτός από την μετάθεση των $A_1,\ldots ,A_m$. Tα πολυώνυμα $p_i(x)^{r_{ij}}$ είναι μονοσήμαντα ορισμένα από τον πίνακα $A$ και λέγονται στοιχειώδεις διαιρέτες του $A$. To γινόμενο των στοιχειωδών διαιρετών του $A$ είναι το χαρακτηριστικό πολυώνυμο του $A$.

Ορισμός 9   O παραπάνω πίνακας λέγεται ρητή κανονική μορφή του πίνακα $A$.

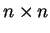
Πόρισμα 3   Δύο $n\times n$ πίνακες είναι όμοιοι αν και μόνο αν έχουν τους ίδιους στοιχειώδεις διαιρέτες

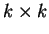
Ορισμός 10   Ένας $k\times k$ πίνακας της μορφής

$$J_{k}(\lambda )=\left(\begin{array}{cccccc} \lambda & 1 & 0 &... ...bda & 1\\ 0 & 0 & 0 & \ldots & 0 & \lambda \end{array}\right)$$

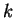
λέγεται στοιχειώδης πίνακας Jordan τάξης $k$ που αντιστοιχεί στην ιδιοτιμή $\lambda$.

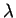
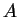
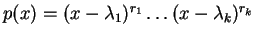
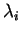
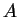
Θεώρημα 17   Aν το ελάχιστο πολυώνυμο ενός πίνακα $Α$ είναι γινόμενο πρωτοβάθμιων παραγόντων $p(x)=(x-\lambda _1)^{r_1}\ldots (x-\lambda _k)^{r_k}$ με τα $\lambda _i$ διαφορετικά μεταξύ τους τότε ο πίνακας $Α$ είναι όμοιος με ένα πίνακα της μορφής

$$\left(\begin{array}{cccc} J_{r_{11},\ldots ,r_{1s_1}}(\lambda... ...ts & J_{r_{k1},\ldots ,r_{ks_k}}(\lambda _k) \end{array}\right)$$

όπου

$$J_{r_{i1},\ldots ,r_{is_i}}(\lambda _i)=\left(\begin{array}{c... ...\ 0 & 0 & \ldots & J_{r_{is_i}}(\lambda _i) \end{array}\right)$$

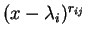
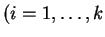
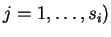
και $(x-\lambda _i)^{r_{ij}}$ $(i=1,\ldots ,k$ $j=1,\ldots ,s_i)$ είναι οι στοιχειώδεις διαιρέτες του $A$. Ο παραπάνω πίνακας λέμε ότι έχει την κανονική μορφή Jordan.

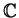
Πόρισμα 4   Κάθε πίνακας με στοιχεία στο $\mathbb C$ είναι όμοιος με ένα πίνακα που έχει την κανονική μορφή Jordan.