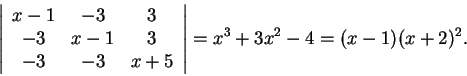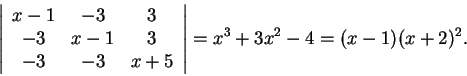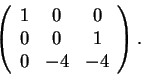Next: Άσκηση 25
Up: Άσκηση 24
Previous: Υπόδειξη
Το χαρακτηριστικό πολυώνυμο του πίνακα είναι το
Εύκολα βλέπει κανείς ότι τα χαρακτηριστικό πολυώνυμο του πίνακα
συμπίπτει με το ελάχιστο και άρα οι στοιχειώδεις διαιρέτες του
πίνακα είναι οι 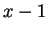 και
και 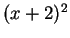 .
Άρα ο πίνακας είναι όμοιος με
τον
.
Άρα ο πίνακας είναι όμοιος με
τον
Vassilis Metaftsis
1999-09-15