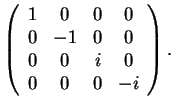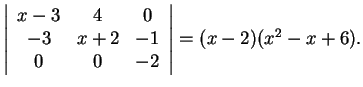 Εύκολα βλέπουμε ότι το χαρακτηριστικό πολυώνυμο συμπίπτει με το
ελάχιστο. Άρα η κανονική ρητή μορφή είναι
Εύκολα βλέπουμε ότι το χαρακτηριστικό πολυώνυμο συμπίπτει με το
ελάχιστο. Άρα η κανονική ρητή μορφή είναι
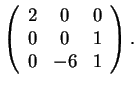 Η Jordan μορφή είναι η
Η Jordan μορφή είναι η
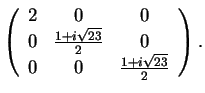
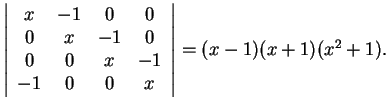 Εύκολα βλέπουμε ότι το ελάχιστο
πολυώνυμο του πίνακα συμπίπτει με το χαρακτηριστικό και άρα η ρητή
μορφή του πίνακα είναι
Εύκολα βλέπουμε ότι το ελάχιστο
πολυώνυμο του πίνακα συμπίπτει με το χαρακτηριστικό και άρα η ρητή
μορφή του πίνακα είναι
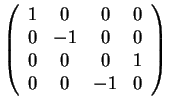 και η κανονική μορφή Jordan είναι
και η κανονική μορφή Jordan είναι