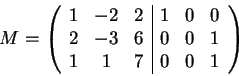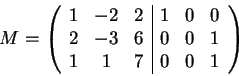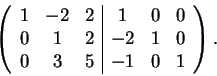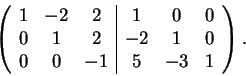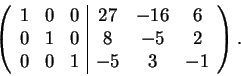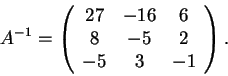Next: Γραμμικές Απεικονίσεις
Up: Άσκηση 33
Previous: Υπόδειξη
Σχηματίζω τον πίνακα
και χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς γραμμών προσπαθώ να
δημιουργήσω τον ταυτοτικό πίνακα 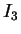 στην αριστερή μεριά. Aρχικά
εφαρμόζω τους μετασχηματισμούς
στην αριστερή μεριά. Aρχικά
εφαρμόζω τους μετασχηματισμούς
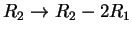 και
και
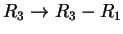 για να πάρω:
για να πάρω:
Στην συνέχεια εφαρμόζω τον
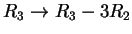 και έχω τον πίνακα
και έχω τον πίνακα
Tώρα χρησιμοποιώ κατα σειρά τους μετασχηματισμούς
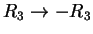 ,
,
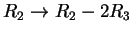
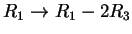 και
και
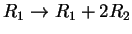 και
παίρνω
και
παίρνω
Άρα,
Vassilis Metaftsis
1999-09-15