


Next: Άσκηση 34
Up: Γραμμικές Απεικονίσεις
Previous: Γραμμικές Απεικονίσεις
Θεώρημα 18
Έστω
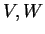
διανυσματικοί χώροι. Aν
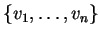
μια βάση του

και
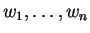
τυχαία στοιχεία του

τότε υπάρχει μια μοναδική
γραμμική απεικόνιση
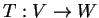
τέτοια ώστε
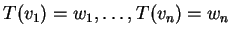
.
Πόρισμα 5
Αν

,

διανυσματικοί χώροι τότε οι
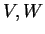
είναι ισομορφικοί αν
και μόνο αν dim
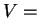
dim

.
Ορισμός 22
Αν
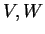
διανυσματικοί χώροι και
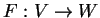
γραμμική απεικόνιση,
ορίζουμε πυρήνα της

(ker

)
το σύνολο των στοιχείων του

που μέσω της

απεικονίζονται στο
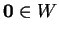
.
Δηλαδή,
Πόρισμα 6
O πυρήνας μιας γραμμικής απεικόνισης
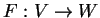
αποτελεί υπόχωρο του

.
Θεώρημα 19
Έστω
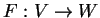
γραμμική απεικόνιση με Ker
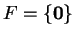
.
Αν

γραμμικώς ανεξάρτητα στοιχεία του

τότε τα
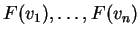
είναι γραμμικώς ανεξάρτητα στοιχεία του

.
Ορισμός 23
Αν
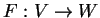
μια γραμμική απεικόνιση ορίζουμε εικόνα της

(Im

)
το σύνολο των στοιχείων του

για τα οποία υπάρχει
στοιχείο

ώστε
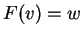
.
Δηλαδή
Πόρισμα 8
Η εικόνα της γραμμικής απεικόνισης
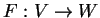
είναι υπόχωρος του

.
Θεώρημα 20
Έστω
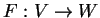
γραμμική απεικόνιση. Τότε
Θεώρημα 21
Έστω
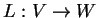
μια γραμμική απεικόνιση. Υποθέτω ότι
dim
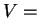
dim

.
Αν Ker
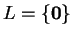
ή Im
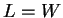
τότε
η
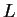
είναι 1-1 και επί.
Θεώρημα 22
Αν
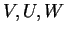
διανυσματικοί χώροι πάνω στο σώμα

.
Έστω
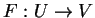
και
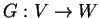
γραμμικές απεικονίσεις. Tότε, η σύνθεση των
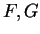
,
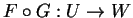
είναι γραμμική απεικόνιση.
Θεώρημα 23
Έστω
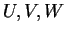
διανυσματικοί χώροι πάνω στο

.
Aν η
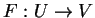
και
οι
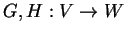
γραμμικές απεικονίσεις τότε
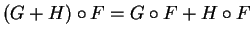
.
Eπιπλέον, αν
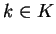
τότε
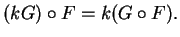
Αν
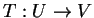
γραμμική απεικόνιση τότε
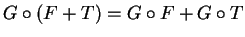
.
Ορισμός 24
Έστω

διανυσματικός χώρος. Μια γραμμική απεικόνιση
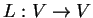
λέγεται τελεστής.
Θεώρημα 24
Αν
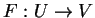
γραμμική απεικόνιση και η
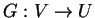
είναι η αντίστροφη
απεικόνιση της

τότε η
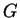
είναι και αυτή γραμμική απεικόνιση.
Πόρισμα 9
Αν
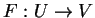
γραμμική απεικόνιση με τετριμμένο πυρήνα η οποία είναι επί.
Τότε η

έχει αντίστροφη γραμμική απεικόνιση.
Ορισμός 25
Αν

ένας
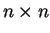
πίνακας, τότε ίχνος του

,
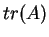
λέμε το
άθροισμα των στοιχείων της κυρίας διαγωνίου
(
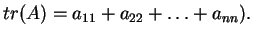



Next: Άσκηση 34
Up: Γραμμικές Απεικονίσεις
Previous: Γραμμικές Απεικονίσεις
Vassilis Metaftsis
1999-09-15
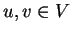 ισχύει
ισχύει
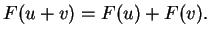
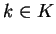 και
και  ισχύει
ισχύει 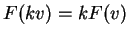 .
.