


Next: Άσκηση 4
Up: Άσκηση 3
Previous: Υπόδειξη
Έστω 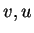 στοιχεία του
στοιχεία του 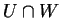 .
Τότε
.
Τότε 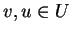 και
και 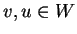 .
Επειδή
.
Επειδή 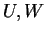 υπόχωροι του
υπόχωροι του  έχω ότι
έχω ότι 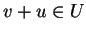 και
και 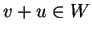 .
Άρα
.
Άρα
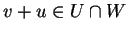 .
Eπίσης, για κάθε
.
Eπίσης, για κάθε  έχω ότι το
έχω ότι το 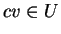 και
και
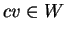 (πάλι διότι oι
(πάλι διότι oι 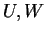 υπόχωροι του
υπόχωροι του  ). Συνεπώς,
). Συνεπώς, 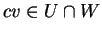 για κάθε
για κάθε 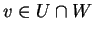 και κάθε
και κάθε  .
Τέλος, το
.
Τέλος, το 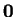 είναι
στοιχείο και του
είναι
στοιχείο και του 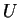 και του
και του  επομένως είναι στοιχείο και του
επομένως είναι στοιχείο και του
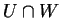 .
Ο
.
Ο 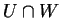 ικανοποιεί τις προϋποθέσεις του ορισμού και
άρα είναι υπόχωρος του διανυσματικού χώρου
ικανοποιεί τις προϋποθέσεις του ορισμού και
άρα είναι υπόχωρος του διανυσματικού χώρου  .
.
Vassilis Metaftsis
1999-09-15