


Next: Άσκηση 37
Up: Άσκηση 36
Previous: Υπόδειξη
Έστω
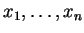 στοιχεία του
στοιχεία του  τέτοια ώστε
τέτοια ώστε
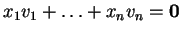 .
Tότε
.
Tότε
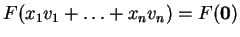 .
Λόγω της
γραμμικότητας της
.
Λόγω της
γραμμικότητας της  η παραπάνω εξίσωση γίνεται
η παραπάνω εξίσωση γίνεται
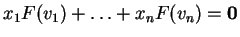 ή ισοδύναμα
ή ισοδύναμα
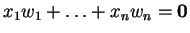 .
Aλλά τα
.
Aλλά τα
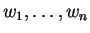 είναι γραμμικώς ανεξάρτητα, άρα η τελευταία
εξίσωση συνεπαγεται ότι
είναι γραμμικώς ανεξάρτητα, άρα η τελευταία
εξίσωση συνεπαγεται ότι
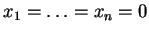 .
Άρα τα
.
Άρα τα
 είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα.
Vassilis Metaftsis
1999-09-15