


Next: Άσκηση 48
Up: Άσκηση 47
Previous: Υπόδειξη
Έστω  .
Tότε το
.
Tότε το 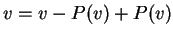 .
Είναι προφανές ότι
.
Είναι προφανές ότι 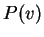 είναι στοιχείο της εικόνας της
είναι στοιχείο της εικόνας της 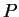 .
Από την άλλη, το
.
Από την άλλη, το 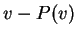 ανήκει στον πυρήνα της
ανήκει στον πυρήνα της 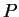 διότι
διότι
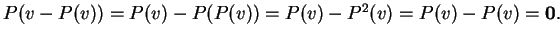 Άρα κάθε
στοιχείο του
Άρα κάθε
στοιχείο του  γράφεται σαν άθροισμα ενός στοιχείου της εικόνας
και ενός στοιχείου του πυρήνα της
γράφεται σαν άθροισμα ενός στοιχείου της εικόνας
και ενός στοιχείου του πυρήνα της 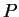 .
Για να δείξω ότι το
άθροισμα είναι ευθύ πρέπει να δείξω ότι
.
Για να δείξω ότι το
άθροισμα είναι ευθύ πρέπει να δείξω ότι
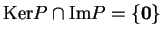 το οποίο είναι προφανές.
το οποίο είναι προφανές.
Vassilis Metaftsis
1999-09-15