


Next: Άσκηση 56
Up: Εσωτερικά Γινόμενα, Καθετότητα
Previous: Εσωτερικά Γινόμενα, Καθετότητα
Παράδειγμα: Aν  είναι ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων μιάς πραγματικής μεταβλητής στο διάστημα
είναι ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων μιάς πραγματικής μεταβλητής στο διάστημα ![$[0,1]$](img840.gif) τότε η απεικόνιση
τότε η απεικόνιση
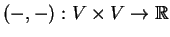 με
με
είναι ένα εσωτερικό γινόμενο στον  .
.
Ορισμός 30
Έστω

είναι ένας διανυσματικός χώρος με εσωτερικό γινόμενο. Λέμε ότι
τα διανύσματα
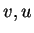
είναι κάθετα μεταξύ τους αν
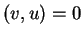
.
Συμβολίζουμε
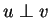
.
Αν
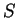
είναι ένα υποσύνολο του

,
συμβολίζουμε
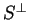
το σύνολο όλων των στοιχείων του

που είναι κάθετα σε όλα τα στοιχεία
του
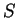
.
Ο
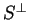
είναι υπόχωρος του

και καλείται ο κάθετος
υπόχωρος του
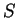
.
Παρατήρηση:
Αν
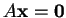 είναι ένα ομογενές
είναι ένα ομογενές 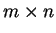 σύστημα, οι λύσεις του
συστήματος, δηλαδή τα διανύσματα
σύστημα, οι λύσεις του
συστήματος, δηλαδή τα διανύσματα
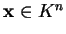 ,
ικανοποιούν τις
εξισώσεις
,
ικανοποιούν τις
εξισώσεις 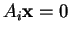
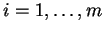 .
To σύνολο των λύσεων του
συστήματος είναι ο κάθετος υπόχωρος του συνόλου
.
To σύνολο των λύσεων του
συστήματος είναι ο κάθετος υπόχωρος του συνόλου
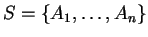 .
.
Ορισμός 31
Έστω

διανυσματικός χώρος με εσωτερικό γινόμενο και
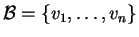
βάση του

.
Η
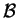
λέγεται ορθογώνια
αν
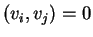
για κάθε
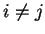
.
Ορισμός 32
Έστω

διανυσματικός χώρος πάνω στο
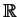
,
με εσωτερικό γινόμενο.
To εσωτερικό γινόμενο λέγεται θετικά ορισμένο αν
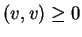
για
κάθε

και
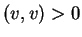
αν
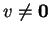
.
Αν

ορίζω νόρμα
του
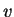
,
Aν
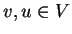
oρίζω απόσταση των
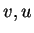
,
Ένα στοιχείο

λέγεται
μοναδιαίο αν
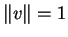
.
Είναι σαφές ότι για κάθε
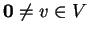
,
το διάνυσμα
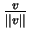
είναι μοναδιαίο.
Θεώρημα 33
Έστω

διανυσματικός χώρος με νόρμα. Για κάθε
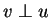
ισχύει το
Πυθαγόρειο Θεώρημα, δηλαδή
Επιπλέον, για τυχαία διανύσματα
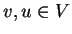
ισχύει ο νόμος του
Παραλληλογράμμου, δηλαδή
Ορισμός 33
Αν

διανυσματικός χώρος με
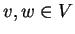
και
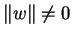
τότε το
λέγεται η προβολή του
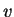
στο
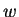
.
Το
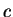
λέγεται το κομμάτι του
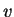
στο
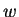
.
Θεώρημα 34 (Ανισότητα Schwarz)
Για κάθε
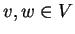
έχουμε
Θεώρημα 35 (Τριγωνική Ανισότητα)
Αν
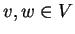
τότε
Θεώρημα 36
Έστω

διανυσματικός χώρος με νόρμα. Έστω

διανύσματα καθετα ανα δύο και τέτοια ώστε
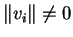
για κάθε
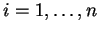
.
Έστω

και
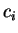
το κομμάτι του
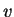
στο
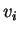
,
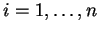
.
Έστω
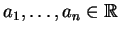
.
Τότε
Θεώρημα 37 (Ανισότητα Bessel)
Έστω

ένας διανυσματικός χώρος με νόρμα και

.
Αν

κάθετα ανα δύο μοναδιαία διανύσματα και αν
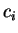
το κομμάτι του
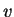
στα
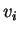
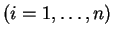
τότε
Παράδειγμα: Av  ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων στο
ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων στο ![$[-\pi,\pi]$](img873.gif) .
Έστω
.
Έστω 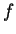 η συνάρτηση με
η συνάρτηση με
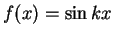 όπου
όπου 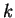 θετικός ακέραιος. Τότε
θετικός ακέραιος. Τότε
Στο συγκεκριμένο παράδειγμα, το κομμάτι της 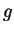 στην
στην 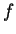 λέγεται
συντελεστής Fourier της
λέγεται
συντελεστής Fourier της 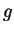 ως προς
ως προς 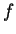 .
Ποιό συγκεκριμένα ο
συντελεστής Fourier είναι
.
Ποιό συγκεκριμένα ο
συντελεστής Fourier είναι
Ορισμός 34
Έστω

διανυσματικός χώρος με θετικά ορισμένο εσωτερικό
γινόμενο. Mια βάση του

έστω
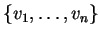
λέγεται
ορθογώνια αν τα στοιχεία της είναι κάθετα ανα δύο, δηλαδή
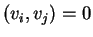
για κάθε
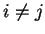
.
Αν επιπλέον τα στοιχεία της
βάσης είναι μοναδιαία διανύσματα τότε η βάση λέγεται ορθοκανονική.
Θεώρημα 38 (Διαδικασία Gram-Schmidt)
Έστω

διανυσματικός χώρος πεπερασμένης διάστασης με θετικά
ορισμένο εσωτερικό γινόμενο. Έστω

υπόχωρος του

και
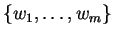
ορθογώνια βάση του

.
Αν
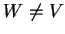
τότε
υπάρχουν στοιχεία
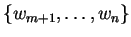
του

ώστε τα
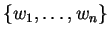
να αποτελούν ορθοκανονική βάση του

.
Πόρισμα 11
Έστω
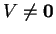
διανυσματικός χώρος πεπερασμένης διάστασης με θετικά ορισμένο
εσωτερικό γινόμενο. To

έχει μια ορθοκανονική βάση.
Θεώρημα 39
Έστω

διανυσματικός χώρος στο
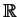
με θετικά ορισμένο εσωτερικό
γινόμενο, διάστασης
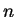
.
Έστω

υπόχωρος του

διάστασης
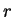
και
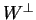
o υπόχωρος του

που αποτελείται από τα στοιχεία
του

κάθετα στα στοιχεία του

.
Τότε το

είναι το ευθύ
άθροισμα των

και
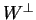
και
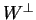
έχει διάσταση
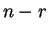
.
Δηλαδή
O υπόχωρος
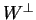
του

λέγεται ορθογώνιο
συμπλήρωμα του

.
Παρατήρηση: Σε έναν διανυσματικό χώρο με ερμιτιανό γινόμενο,
οι έννοιες ορθογωνιότητας, καθετότητας και οι έννοιες της ορθογώνιας και
ορθοκανονικής βάσης καθώς και το ορθογώνιο συμπλήρωμα ενός υπόχωρου
ορίζονται κατα τον ίδιο ακριβώς τρόπο όπως και στην περίπτωση του
διανυσματικού χώρου με εσωτερικό γινόμενο.
Θεώρημα 40 (Διαδικασία Gram-Schmidt)
Έστω

διανυσματικός χώρος πεπερασμένης διάστασης με θετικά
ορισμένο ερμιτιανό γινόμενο. Έστω

υπόχωρος του

και
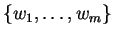
ορθογώνια βάση του

.
Αν
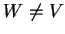
τότε
υπάρχουν στοιχεία
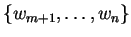
του

ώστε τα
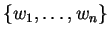
να αποτελούν ορθοκανονική βάση του

.
Πόρισμα 12
Έστω
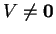
διανυσματικός χώρος πεπερασμένης διάστασης με θετικά ορισμένο
ερμιτιανό γινόμενο, πάνω στο
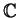
.
To

έχει μια ορθοκανονική βάση.
Θεώρημα 41
Έστω

διανυσματικός χώρος στο
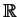
με θετικά ορισμένο εσωτερικό
γινόμενο, ή στο
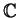
με θετικά ορισμένο ερμιτιανό γινόμενο. Έστω
ότι η διάσταση του

είναι πεπερασμένη, ίση με
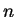
.
Έστω

είναι υπόχωρος του

διάστασης
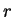
και
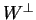
o υπόχωρος του

που αποτελείται από τα στοιχεία του

κάθετα στα στοιχεία
του

.
Τότε το

είναι το ευθύ άθροισμα των

και
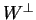
και
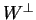
έχει διάσταση
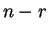
.
Δηλαδή
Θεώρημα 42
Έστω το σύστημα γραμμικών εξισώσεων
Οι λύσεις του συστήματος μπορούν να ερμηνευθούν με τους παρακάτω τρόπους
- .
- Eίναι τα διανύσματα που ικανοποιούν την εξίσωση
- .
- Eίναι τα στοιχεία του ορθογώνιου υπόχωρου στα διανύσματα γραμμές του
συστήματος.
- .
- Είναι τα στοιχεία του πυρήνα της γραμμικής απεικόνισης που αντιστοιχεί
στον πίνακα
 ,
δηλαδή οι λύσεις της εξίσωσης
,
δηλαδή οι λύσεις της εξίσωσης 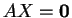 .
.
Ορισμός 36
Αν

είναι ένας
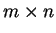
πίνακας με στοιχεία στο

,
τότε οι
στήλες του

,
έστω
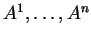
ορίζουν έναν υπόχωρο του
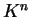
η διάσταση του οποίου καλείται τάξη στηλών του

.
Όμοια, η διάσταση του υπόχωρου που ορίζουν οι γραμμές
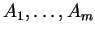 του
του  λέγεται τάξη γραμμών του
λέγεται τάξη γραμμών του  .
.
Θεώρημα 43
Αν

ένας
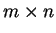
πίνακας. Τότε η τάξη γραμμών και η τάξη στηλών του

είναι ίσες, έστω
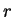
.
Επιπλέον, η διάσταση του υπόχωρου των λύσεων
του ομογενούς συστήματος που αντιστοιχεί στον

είναι
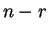
.



Next: Άσκηση 56
Up: Εσωτερικά Γινόμενα, Καθετότητα
Previous: Εσωτερικά Γινόμενα, Καθετότητα
Vassilis Metaftsis
1999-09-15
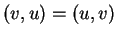 για κάθε
για κάθε 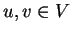
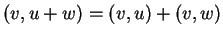 για κάθε
για κάθε 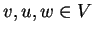
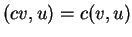 και
και 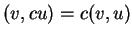 για κάθε
για κάθε 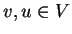 και κάθε
και κάθε  .
.
![]() είναι ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων μιάς πραγματικής μεταβλητής στο διάστημα
είναι ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων μιάς πραγματικής μεταβλητής στο διάστημα ![]() τότε η απεικόνιση
τότε η απεικόνιση
![]() με
με
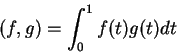
![]() είναι ένα ομογενές
είναι ένα ομογενές ![]() σύστημα, οι λύσεις του
συστήματος, δηλαδή τα διανύσματα
σύστημα, οι λύσεις του
συστήματος, δηλαδή τα διανύσματα
![]() ,
ικανοποιούν τις
εξισώσεις
,
ικανοποιούν τις
εξισώσεις ![]()
![]() .
To σύνολο των λύσεων του
συστήματος είναι ο κάθετος υπόχωρος του συνόλου
.
To σύνολο των λύσεων του
συστήματος είναι ο κάθετος υπόχωρος του συνόλου
![]() .
.
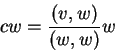
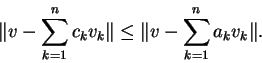
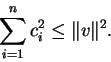
![]() ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων στο
ο διανυσματικός χώρος όλων των
συνεχών συναρτήσεων στο ![]() .
Έστω
.
Έστω ![]() η συνάρτηση με
η συνάρτηση με
![]() όπου
όπου ![]() θετικός ακέραιος. Τότε
θετικός ακέραιος. Τότε
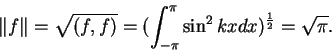
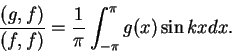
![]() για κάθε
για κάθε ![]() και
και ![]() για κάθε
για κάθε ![]() .
.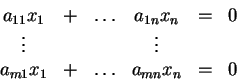
![]() του
του ![]() λέγεται τάξη γραμμών του
λέγεται τάξη γραμμών του ![]() .
.