


Next: Άσκηση 63
Up: Άσκηση 62
Previous: Υπόδειξη
Έστω
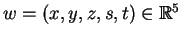 τέτοιο ώστε
τέτοιο ώστε 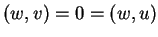 ,
δηλαδή
,
δηλαδή
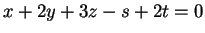 και
και
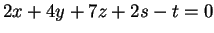 .
Λύνοντας ως προς
.
Λύνοντας ως προς 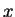 την πρώτη
εξίσωση και αντικαθιστώντας στην δεύτερη παίρνω το σύστημα
την πρώτη
εξίσωση και αντικαθιστώντας στην δεύτερη παίρνω το σύστημα
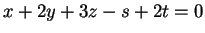 ,
,
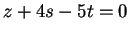 .
Αν θεωρήσω τα
.
Αν θεωρήσω τα 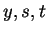 σαν ελεύθερες μεταβλητές
τότε ο υπόχωρος
σαν ελεύθερες μεταβλητές
τότε ο υπόχωρος 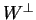 είναι διάστασης 3 και άρα τα διανύσματα
είναι διάστασης 3 και άρα τα διανύσματα
είναι μια βάση του 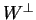 .
.
Vassilis Metaftsis
1999-09-15