


Next: Άσκηση 64
Up: Άσκηση 63
Previous: Υπόδειξη
Θα δείξω πρώτα ότι
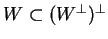 .
Έστω
.
Έστω 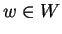 .
Τότε
.
Τότε
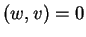 για κάθε
για κάθε
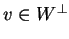 .
Άρα,
.
Άρα,
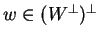 .
Ξέρω ότι ισχύει
.
Ξέρω ότι ισχύει
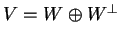 .
Από την άλλη, ο
.
Από την άλλη, ο 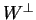 είναι υπόχωρος του
είναι υπόχωρος του  και άρα ισχύει
και άρα ισχύει
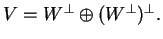 Άρα, dim
Άρα, dim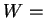 dim
dim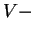 dim
dim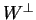 ,
και dim
,
και dim
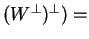 dim
dim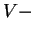 dim
dim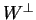 .
Άρα
dim
.
Άρα
dim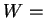 dim
dim
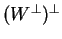 και λόγω του ότι
και λόγω του ότι
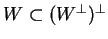 έχω ότι
έχω ότι
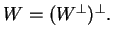
Vassilis Metaftsis
1999-09-15