


Next: Άσκηση 1
Up: Διανυσματικοί Χώροι
Previous: Διανυσματικοί Χώροι
Tα σύνολα 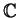 και
και 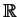 είναι σώματα ενώ το
είναι σώματα ενώ το 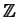 δεν είναι σώμα.
To σύνολο
δεν είναι σώμα.
To σύνολο 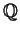 όλων των ρητών αριθμών είναι σώμα.
όλων των ρητών αριθμών είναι σώμα.
Ορισμός 2
Aν
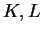
σώματα και το

περιέχεται στο
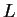
τότε λέμε ότι το

είναι
υπόσωμα του
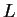
.
Το 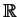 είναι υπόσωμα του
είναι υπόσωμα του 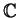 και το
και το 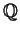 είναι υπόσωμα του
είναι υπόσωμα του 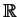 .
.
Λέμε συνήθως ότι ο  είναι διανυσματικός χώρος και εννοούμε ότι ο
είναι διανυσματικός χώρος και εννοούμε ότι ο  είναι διανυσματικός χώρος πάνω στο
είναι διανυσματικός χώρος πάνω στο  .
Τα στοιχεία του
.
Τα στοιχεία του  λέγονται
διανύσματα
λέγονται
διανύσματα
Ορισμός 5
Έστω

ένας διανυσματικός χώρος και
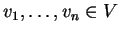
.
Αν
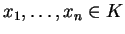
τότε μια έκφραση της μορφής
καλείται γραμμικός συνδυασμός των

.
Θεώρημα 1
Έστω

το σύνολο όλων των γραμμικών συνδυασμών των στοιχείων

του

.
Tότε το

έιναι υπόχωρος του

.
O παραπάνω υπόχωρος  καλείται ο υπόχωρος που παράγεται από τα
καλείται ο υπόχωρος που παράγεται από τα
 .
Aν ο
.
Aν ο 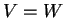 τότε λέμε ότι ο
τότε λέμε ότι ο  παράγεται από
τα
παράγεται από
τα
 .
.
Παραδείγματα 1. Αν 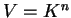 είναι το σύνολο όλων των
είναι το σύνολο όλων των
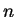 -άδων στοιχείων του
-άδων στοιχείων του  .
Αν
.
Αν
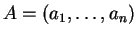 και
και
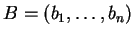 στοιχεία του
στοιχεία του  ,
oρίζουμε
,
oρίζουμε
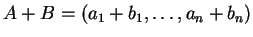 και
και
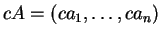 για
κάθε
για
κάθε  .
Tότε το
.
Tότε το  με τις παραπάνω πράξεις είναι
διανυσματικός χώρος πάνω στο
με τις παραπάνω πράξεις είναι
διανυσματικός χώρος πάνω στο  .
.
2. Αν  διανυσματικός χώρος και
διανυσματικός χώρος και 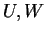 υπόχωροι του
υπόχωροι του  ,
τότε το
,
τότε το
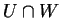 είναι υπόχωρος του
είναι υπόχωρος του  .
.
3. Αν 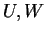 υπόχωροι του διανυσματικού χώρου
υπόχωροι του διανυσματικού χώρου  τότε ορίζω με
τότε ορίζω με 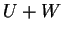 να είναι το σύνολο όλων των στοιχείων του
να είναι το σύνολο όλων των στοιχείων του  της μορφής
της μορφής 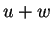 όπου
όπου
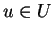 και
και 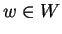 .
Το
.
Το 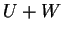 είναι υπόχωρος του
είναι υπόχωρος του  .
.
Ορισμός 6
Έστω

ένας διανυσματικός χώρος πάνω στο σώμα

και έστω

στοιχεία του

.
Λέμε ότι τα

είναι γραμμικώς εξαρτημένα αν υπάρχουν στοιχεία
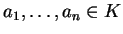
όχι όλα ίσα με το μηδεν τέτοια ώστε
Στην αντίθετη περίπτωση λέμε ότι τα στοιχεία
 είναι
γραμμικώς ανεξάρτητα. Δηλαδή:
είναι
γραμμικώς ανεξάρτητα. Δηλαδή:
Ορισμός 7
Tα στοιχεία

ενός διανυσματικού χώρου

λέγονται
γραμμικώς ανεξάρτητα αν για κάθε
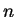
-άδα αριθμών
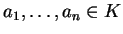
για την οποία ισχύει
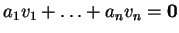
συνεπάγεται
ότι
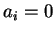
για κάθε
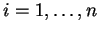
.
Παράδειγμα: Αν 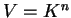 τότε τα διανύσματα
τότε τα διανύσματα
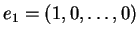 ,
,
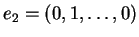 ,
,
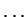 ,
,
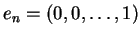 είναι γραμμικώς
ανεξάρτητα.
είναι γραμμικώς
ανεξάρτητα.
Ορισμός 8
Aν

είναι στοιχεία του

τα οποία παράγουν τον

και
είναι γραμμικώς ανεξάρτητα τότε λέμε ότι το σύνολο
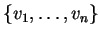
είναι μια βάση του

.
Τα στοιχεία

λέμε ότι αποτελούν
βάση του

.
Παράδειγμα: Aν 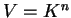 τότε τα στοιχεία
τότε τα στοιχεία
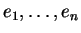 που
ορίσαμε παραπάνω αποτελούν βάση του
που
ορίσαμε παραπάνω αποτελούν βάση του  .
.
Θεώρημα 2
Έστω

διανυσματικός χώρος και

γραμμικώς ανεξάρτητα
στοιχεία του

.
Έστω
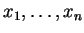
και
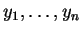
στοιχεία
του

.
Αν
τότε
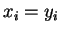
για κάθε
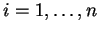
.
Ορισμός 9
Έστω

ένας διανυσματικός χώρος και
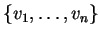
υποσύνολο του

.
Aν
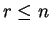
λέμε ότι το σύνολο
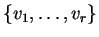
είναι ένα μεγιστικό
υποσύνολο από γραμμικώς ανεξάρτητα διανύσματα αν τα στοιχεία
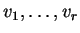
είναι γραμμικώς ανεξάρτητα και τα στοιχεία
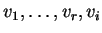
είναι γραμμικώς εξαρτημένα για κάθε
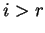
.
Ορισμός 10
Αν

διανυσματικός χώρος, λέμε ότι τα

παράγουν
τον

αν κάθε στοιχείο του

γράφετε σαν γραμμικώς συνδυασμός
των

.
Το σύνολο
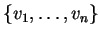
λέγεται
σύνολο γεννητόρων του

.
Θεώρημα 3
Έστω
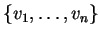
ένα σύνολο γεννητόρων του

και έστω
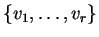
ένα μεγιστικό υποσύνολο από γραμμικώς
ανεξάρτητων στοιχείa του

.
Τότε το
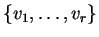
είναι μια
βάση του

.
Θεώρημα 4
Έστω

διανυσματικός χώρος πάνω στο σώμα

.
Έστω
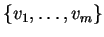
μια βάση του

.
Aν
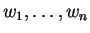
είναι στοιχεία του

και
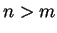
τότε τα
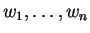
είναι γραμμικώς
εξαρτημένα.
Θεώρημα 5
Έστω

διανυσματικός χώρος με μια βάση που αποτελείται από
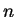
στοιχεία
και μια βάση που αποτελείται από
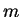
στοιχεία. Τότε
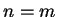
.
Ορισμός 11
Έστω

διανυσματικός χώρος και
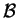
μια βάση του

που
αποτελείται από
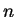
στοιχεία. Το
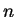
καλείται διάσταση του

.
Aν
το
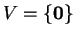
τότε το

δεν έχει βάση και η διάστασή του είναι
μηδέν. Αν η βάση του

αποτελείται από πεπερασμένο αριθμό
στοιχείων λέμε ότι ο χώρος έχει πεπερασμένη διάσταση. Στην
αντίθετη περίπτωση λέμε ότι ο χώρος ειναι άπειρης διάστασης. H
διάσταση του

συμβολίζεται με dim

.
Παραδειγμα: Aν 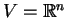 τότε η διάσταση του
τότε η διάσταση του  είναι
είναι
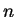 εφόσον το
εφόσον το
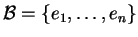 είναι μια βάση του
είναι μια βάση του  .
.
Ορισμός 12
Έτσω

γραμμικώς ανεξάρτητα διανύσματα ενός διανυσματικού
χώρου

.
Τα στοιχεία
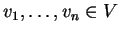
αποτελούν ένα μεγιστικό
σύνολο γραμμικώς ανεξάρτητων στοιχείων του

αν για κάθε στοιχείο
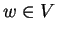
τα στοιχεία
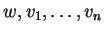
είναι γραμμικώς εξαρτημένα.
Θεώρημα 6
Aν

διανυσματικός χώρος και
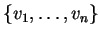
ένα μεγιστικό
υποσύνολο γραμμικώς ανεξάρτητων στοιχείων του

τότε το σύνολο
αποτελεί βάση του

.
Θεώρημα 7
Έστω

διανυσματικός χώρος διάστασης
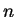
και

γραμμικώς ανεξάρτητα στοιχεία του

.
Τότε τα

αποτελούν βάση του

.
Πόρισμα 1
Έστω

διανυσματικός χώρος και

υπόχωρος του

ώστε
dim
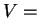
dim

τότε
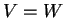
.
Πόρισμα 2
Έστω

διανυσματικός χώρος διάστασης
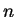
.
Έστω
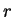
θετικός ακέραιος με
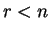
και
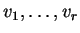
γραμμικώς ανεξάρτητα στοιχεία του

.
Τότε
μπορούμε να βρούμε στοιχεία
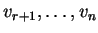
στον

ώστε τα

να αποτελούν βάση του

.
Θεώρημα 8
Έστω

διανυσματικός χώρος με βάση που αποτελείται απο
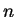
στοιχεία.
Έστω

υπόχωρος του

που δεν αποτελείται μόνο από το
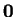
.
Τότε το

έχει μιά βάση που αποτελέιται απο το πολύ
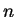
στοιχεία.
Ορισμός 13
Aν

διανυσματικός χώρος και
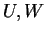
υπόχωροι του

τέτοιοι ώστε
κάθε στοιχείο

γράφεται κατά μοναδικό τρόπο
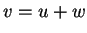
όπου
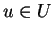
και
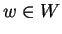
τότε το

λέγεται το ευθύ άθροισμα των
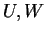
.
Θεώρημα 9
Έστω

διανυσματικός χώρος πάνω στο

και
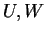
υπόχωροι του

.
Aν
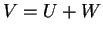
και
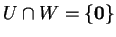
τότε το

είναι το ευθύ
άθροισμα των
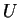
και

.
Το ευθύ άθροισμα συμβολίζεται
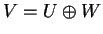
.
Θεώρημα 10
Έστω

ένας διανυσματικός χώρος με πεπερασμένη διάσταση πάνω στο
σώμα

και

ένας υπόχωρος του

.
Tότε υπάρχει υπόχωρος του

,
έστω
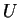
,
τέτοιος ώστε το

να είναι το ευθύ άθροισμα των
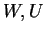
.
Θεώρημα 11
Έστω

ένας διανυσματικός χώρος με πεπερασμένη διάσταση πάνω στο
σώμα

με
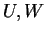
υπόχωρους τέτοιους ώστε
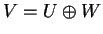
.
Τότε



Next: Άσκηση 1
Up: Διανυσματικοί Χώροι
Previous: Διανυσματικοί Χώροι
Vassilis Metaftsis
1999-09-15
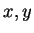 στοιχεία του
στοιχεία του  τότε και το
τότε και το 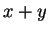 είναι στοιχείο του
είναι στοιχείο του  .
.
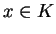 τότε και το
τότε και το 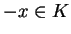 .
Επιπλέον αν
.
Επιπλέον αν 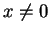 τότε το
τότε το
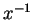 είναι στοιχείο του
είναι στοιχείο του  .
.
 .
.
![]() και
και ![]() είναι σώματα ενώ το
είναι σώματα ενώ το ![]() δεν είναι σώμα.
To σύνολο
δεν είναι σώμα.
To σύνολο ![]() όλων των ρητών αριθμών είναι σώμα.
όλων των ρητών αριθμών είναι σώμα.
![]() είναι υπόσωμα του
είναι υπόσωμα του ![]() και το
και το ![]() είναι υπόσωμα του
είναι υπόσωμα του ![]() .
.
![]() είναι διανυσματικός χώρος και εννοούμε ότι ο
είναι διανυσματικός χώρος και εννοούμε ότι ο ![]() είναι διανυσματικός χώρος πάνω στο
είναι διανυσματικός χώρος πάνω στο ![]() .
Τα στοιχεία του
.
Τα στοιχεία του ![]() λέγονται
διανύσματα
λέγονται
διανύσματα
![]() καλείται ο υπόχωρος που παράγεται από τα
καλείται ο υπόχωρος που παράγεται από τα
![]() .
Aν ο
.
Aν ο ![]() τότε λέμε ότι ο
τότε λέμε ότι ο ![]() παράγεται από
τα
παράγεται από
τα
![]() .
.
![]() είναι το σύνολο όλων των
είναι το σύνολο όλων των
![]() -άδων στοιχείων του
-άδων στοιχείων του ![]() .
Αν
.
Αν
![]() και
και
![]() στοιχεία του
στοιχεία του ![]() ,
oρίζουμε
,
oρίζουμε
![]() και
και
![]() για
κάθε
για
κάθε ![]() .
Tότε το
.
Tότε το ![]() με τις παραπάνω πράξεις είναι
διανυσματικός χώρος πάνω στο
με τις παραπάνω πράξεις είναι
διανυσματικός χώρος πάνω στο ![]() .
.
![]() διανυσματικός χώρος και
διανυσματικός χώρος και ![]() υπόχωροι του
υπόχωροι του ![]() ,
τότε το
,
τότε το
![]() είναι υπόχωρος του
είναι υπόχωρος του ![]() .
.
![]() υπόχωροι του διανυσματικού χώρου
υπόχωροι του διανυσματικού χώρου ![]() τότε ορίζω με
τότε ορίζω με ![]() να είναι το σύνολο όλων των στοιχείων του
να είναι το σύνολο όλων των στοιχείων του ![]() της μορφής
της μορφής ![]() όπου
όπου
![]() και
και ![]() .
Το
.
Το ![]() είναι υπόχωρος του
είναι υπόχωρος του ![]() .
.
![]() είναι
γραμμικώς ανεξάρτητα. Δηλαδή:
είναι
γραμμικώς ανεξάρτητα. Δηλαδή:
![]() τότε τα διανύσματα
τότε τα διανύσματα
![]() ,
,
![]() ,
,
![]() ,
,
![]() είναι γραμμικώς
ανεξάρτητα.
είναι γραμμικώς
ανεξάρτητα.
![]() τότε τα στοιχεία
τότε τα στοιχεία
![]() που
ορίσαμε παραπάνω αποτελούν βάση του
που
ορίσαμε παραπάνω αποτελούν βάση του ![]() .
.
![]() τότε η διάσταση του
τότε η διάσταση του ![]() είναι
είναι
![]() εφόσον το
εφόσον το
![]() είναι μια βάση του
είναι μια βάση του ![]() .
.