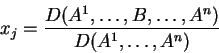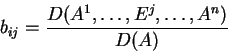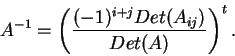Next: Άσκηση 68
Up: Ορίζουσες
Previous: Ορίζουσες
O ορισμός της 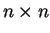 ορίζουσας είναι επαγωγικός
ορίζουσας είναι επαγωγικός
Ορισμός 37
Αν

είναι ο
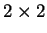
πίνακας
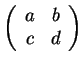
με στοιχεία στο σώμα

.
Ορίζουμε την ορίζουσα του

,
Υποθέτω ότι έχει ορισθεί η ορίζουσα των
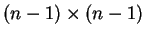
πινάκων. Τότε,
αν

είναι ένας
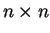
πίνακας ορίζουμε
Tο παραπάνω λέγεται το ανάπτυγμα της ορίζουσας ως προς την
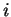
γραμμή.
Θεώρημα 44
H ορίζουσα ικανοποιεί τον ορισμό του αναπτύγματος, για κάθε στήλη και για
κάθε γραμμή της ορίζουσας δηλαδή
H ορίζουσα κάθε πίνακα είναι ίση με την
ορίζουσα του ανάστροφου του, δηλαδή
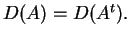
Θεώρημα 46 (Κανόνας Cramer)
Έστω
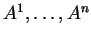
διανύσματα στήλες τέτοια ώστε
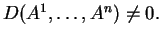
Έστω
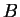
διάνυσμα στήλη. Aν
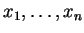
στοιχεία του

τέτοια ώστε
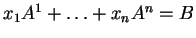
τότε για κάθε
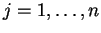
έχουμε
όπου η στήλη
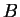
εμφανίζεται στην
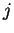
στήλη στην θέση της
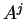
.
Θεώρημα 47
Έστω
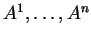
διανύσματα στήλες διάστασης
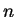
.
Aν τα διανύσματα
είναι γραμμικώς εξαρτημένα τότε
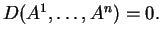
Αν
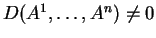
τότε τα
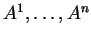
είναι γραμμικώς
ανεξάρτητα.
Πόρισμα 13
Αν
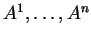
είναι διανύσματα στήλες του
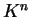
τέτοια ώστε
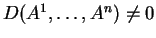
και
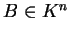
τότε υπάρχουν
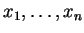
τέτοια ώστε
Θεώρημα 48
Η ορίζουσα
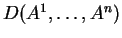
είναι μηδέν αν και μόνο αν τα
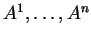
είναι γραμμικώς εξαρτημένα.
Θεώρημα 49
Aν
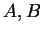
είναι
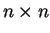
πίνακες τότε
Πόρισμα 14
Αν

ένας
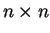
αντιστρέψιμος πίνακας τότε
Θεώρημα 50
Έστω
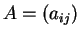
ένας
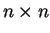
πίνακας και
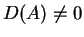
.
Τότε ο

είναι
αντιστρέψιμος. Επιπλέον, αν
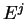
είναι τα μοναδιαία διανύσματα στήλες και
τότε ο
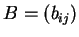
είναι ο αντίστροφος του

.
Δηλαδή



Next: Άσκηση 68
Up: Ορίζουσες
Previous: Ορίζουσες
Vassilis Metaftsis
1999-09-15
![]() ορίζουσας είναι επαγωγικός
ορίζουσας είναι επαγωγικός
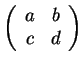 με στοιχεία στο σώμα
με στοιχεία στο σώμα 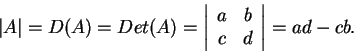
![]() τότε
τότε