


Next: Άσκηση 19
Up: Άσκηση 18
Previous: Υπόδειξη
Έστω
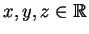 με
με
. Η παραπάνω εξίσωση
ισχύει για κάθε
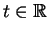 .
Στην παραπάνω εξίσωση αντικαταθηστώ
.
Στην παραπάνω εξίσωση αντικαταθηστώ
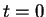 και παίρνω
και παίρνω 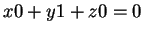 και άρα
και άρα 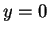 .
Aν αντικαταστήσω
.
Aν αντικαταστήσω
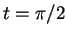 τότε παίρνω
τότε παίρνω
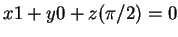 και άρα
και άρα 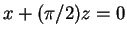 .
Tέλος, αν θέσω
.
Tέλος, αν θέσω 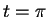 έχω
έχω
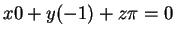 ή ισοδύναμα
ή ισοδύναμα 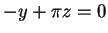 .
Η τελευταία αυτή εξίσωση, σε συνδυασμό με το ότι
.
Η τελευταία αυτή εξίσωση, σε συνδυασμό με το ότι 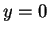 έχω
έχω
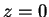 και άρα και
και άρα και 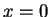 .
Eπομένως τα
.
Eπομένως τα 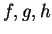 γραμμικώς ανεξάρτητα.
γραμμικώς ανεξάρτητα.
Vassilis Metaftsis
1999-09-15