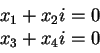Next: Άσκηση 20
Up: Άσκηση 19
Previous: Υπόδειξη
Θα δείξουμε ότι η
είναι μια βάση του  .
Έστω ένα
.
Έστω ένα  .
Tότε το
.
Tότε το 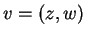 όπου
όπου
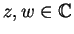 .
Άρα το
.
Άρα το 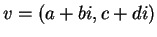 ,
όπου
,
όπου
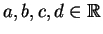 .
Tότε το
.
Tότε το
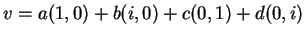 άρα το
άρα το 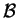 παράγει το
παράγει το  .
Θα δείξουμε ότι τα στοιχεία του
.
Θα δείξουμε ότι τα στοιχεία του 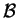 είναι γραμμικώς
ανεξάρτητα. Έστω
είναι γραμμικώς
ανεξάρτητα. Έστω
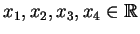 ώστε
ώστε
Τότε, το σύστημα
που παίρνουμε είναι
το οποίο φυσικά δίνει
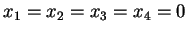 και άρα τα
στοιχεία του
και άρα τα
στοιχεία του 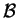 είναι γραμμικώς ανεξάρτητα. Κατα συνέπεια,
dim(
είναι γραμμικώς ανεξάρτητα. Κατα συνέπεια,
dim(
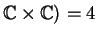 .
.
Vassilis Metaftsis
1999-09-15