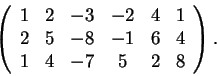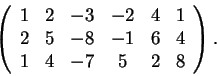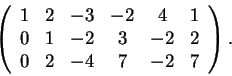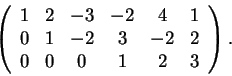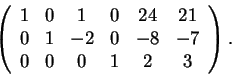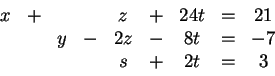Next: Άσκηση 31
Up: Άσκηση 30
Previous: Υπόδειξη
O επαυξημένος πίνακας του συστήματος είναι ο πίνακας
Με οδηγό στοιχείο το 1 της θέσης 11 και τους μετασχηματισμούς
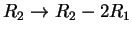 και
και
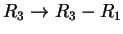 παίρνω τον ισοδύναμο πίνακα
παίρνω τον ισοδύναμο πίνακα
Χρησιμοποιώντας το 1 της θέσης 22 και τον μετασχηματισμό
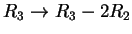 έχω τον πίνακα
έχω τον πίνακα
O τελευταίος αυτός πίνακας δεν είναι η αναγμένη μορφή του αρχικού μιας
και στις στήλες των ηγετικών 1 υπάρχουν μη-μηδενικά στοιχεία. Για
να πάρω την αναγμένη μορφή χρησιμοποιώ με την σειρά τους μετασχηματισμούς
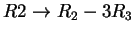 ,
,
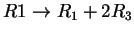 και
και
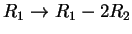 και έχω
και έχω
To σύστημα στο οποίο αναγώμαστε είναι το
από το οποίο παίρνουμε τις λύσεις 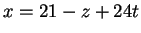 ,
,
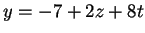 και
και 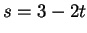 .
.
Vassilis Metaftsis
1999-09-15