

Next: Άσκηση 1
Up: No Title
Previous: Λύση
Ορισμός 14
Λέμε οτι ((τα
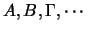
αποτελούν
κάλυψη του

)) αν
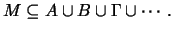
Αν το πλήθος των
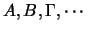
είναι πεπερασμένο τότε λέμε οτι αποτελούν
πεπερασμένη κάλυψη του

.
Αν
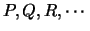
είναι μερικά από τα
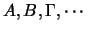
και τα
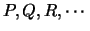
επίσης αποτελούν κάλυψη του

τότε λέμε οτι ((τα
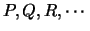
αποτελούν
υπο-κάλυψη του

))
ή ότι ((η κάλυψη
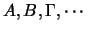
του

περιέχει την υποκάλυψη
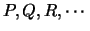
του

)).
Αν επιπλέον το πλήθος των
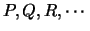
είναι πεπερασμένο τότε λέμε οτι ((η κάλυψη
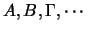
του

περιέχει την πεπερασμένη υπο-κάλυψη
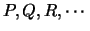
του

)).
Ορισμός 15
Έστω οτι
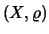
είναι, μετρικός χώρος. Αν τα
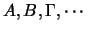
αποτελούν κάλυψη του

και όλα τα
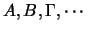
είναι ανοικτά
υποσύνολα του
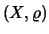
τότε λέμε οτι ((τα
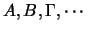
αποτελούν
ανοικτή κάλυψη του

)).
Ορισμός 16
Έστω

υποσύνολο μετρικού χώρου
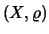
.
Το

λέγεται
φραγμένο αν
υπάρχει
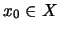
και θετικός αριθμός
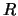
ώστε
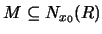
.
Αν ένα σύνολο
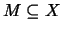
,
όπου
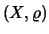
μετρικός χώρος, είναι συμπαγές τότε το

είναι κλειστό και φραγμένο.
Το αντίστροφο δεν είναι πάντα σωστό. Το αντίστροφο ισχύει όμως όταν ο
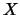
είναι ο
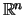
με την συνήθη μετρική (Θεώρημα
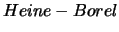
).
Αν το
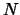
είναι κλειστό υποσύνολο του συμπαγούς

τότε και το
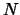
είναι συμπαγές.
Θεώρημα 17
Έστω υποσύνολο

του
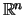
.
Το

είναι συμπαγές αν και μόνο αν οποιαδήποτε ακολουθία στο

έχει υποακολουθία που συγκλίνει σε στοιχείο του

.
Μια συνέπεια αυτού του θεωρήματος είναι ότι κάθε μη κενό και συμπαγές υποσύνολο του
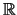
έχει μέγιστο και ελάχιστο στοιχείο. Παρατηρούμε
εδώ ότι το παραπάνω θεώρημα ισχύει και σε γενικούς μετρικούς χώρους και όχι μόνο στον
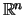
.
Θεώρημα 18
Έστω

συμπαγές υποσύνολο του
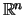
και συνάρτηση
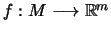
συνεχής στο

.
Τότε το
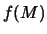
είναι συμπαγές υποσύνολο του
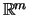
.
Δηλαδή ((η συνεχής εικόνα συμπαγούς συνόλου είναι συμπαγές σύνολο))
και αυτό το θεώρημα συνεχίζει να ισχύει στους γενικούς μετρικούς χώρους.
Ορισμός 19
Έστω μετρικοί χώροι
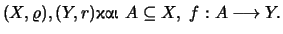
Η
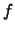
λέγεται
ομοιόμορφα συνεχής στο
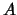
αν για κάθε
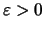
υπάρχει
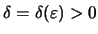
ώστε
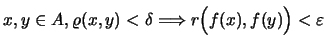
.
Πρόταση 20
'Εστω

συμπαγές υποσύνολο του
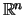
και συνάρτηση
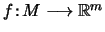
συνεχής στο

.
Τότε
η
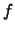
είναι ομοιόμορφα συνεχής.
root
1999-07-29