ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
- ΟΡΙΣΜΟΙ
Έστω
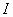 ανοιχτό
διάστημα (φραγμένο ή μη) (
ανοιχτό
διάστημα (φραγμένο ή μη) (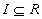 )
και
)
και 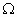 ανοιχτό υποσύνολο του
ανοιχτό υποσύνολο του 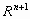 ,
,
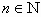 .
.
Ορισμός 1:
Αν 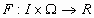 είναι μια πραγματική
συνάρτηση
είναι μια πραγματική
συνάρτηση 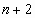 μεταβλητών
και
μεταβλητών
και 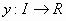 μια
άγνωστη συνάρτηση, η εξίσωση
μια
άγνωστη συνάρτηση, η εξίσωση
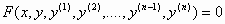 , (1)
, (1)
όπου
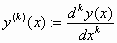 ,
, 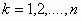 ,
ονομάζεται συνήθης
διαφορική εξίσωση (Σ.Δ.Ε.).
,
ονομάζεται συνήθης
διαφορική εξίσωση (Σ.Δ.Ε.).
Ορισμός 2
: Η (1)
ονομάζεται Σ.Δ.Ε. τάξης 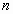 όταν η συνάρτηση
όταν η συνάρτηση 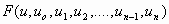 δεν είναι σταθερή ως προς
τη μεταβλητή
δεν είναι σταθερή ως προς
τη μεταβλητή 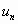 , δηλ.
όταν η μεγαλύτερης τάξης παράγωγος της
άγνωστης συνάρτησης που εμφανίζεται στην
εξίσωση είναι η
, δηλ.
όταν η μεγαλύτερης τάξης παράγωγος της
άγνωστης συνάρτησης που εμφανίζεται στην
εξίσωση είναι η 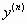 .
.
Ορισμός 3
: Ονομάζουμε
λύση της (1) κάθε
πραγματική συνάρτηση 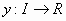 η οποία είναι
η οποία είναι 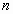 φορές παραγωγίσιμη στο
φορές παραγωγίσιμη στο 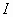 ενώ παράλληλα για κάθε
ενώ παράλληλα για κάθε 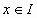 ισχύουν τα εξής:
ισχύουν τα εξής:
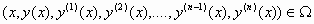 ,
,
και
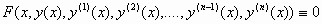 .
.
Το
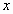 στην
εξίσωση (1) ονομάζεται ανεξάρτητη
μεταβλητή και το
στην
εξίσωση (1) ονομάζεται ανεξάρτητη
μεταβλητή και το 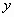 άγνωστη συνάρτηση. Το
γράφημα μιας λύσης
άγνωστη συνάρτηση. Το
γράφημα μιας λύσης 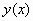 ονομάζεται ολοκληρωτική
καμπύλη της (1).
ονομάζεται ολοκληρωτική
καμπύλη της (1).
Ορισμός 4
: Αν μια Σ.Δ.Ε.
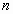 τάξης
μπορεί να γραφεί στη μορφή
τάξης
μπορεί να γραφεί στη μορφή
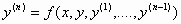 , (2)
, (2)
όπου
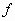 είναι
μια πραγματική συνάρτηση ορισμένη σ’ ένα
ανοικτό υποσύνολο
είναι
μια πραγματική συνάρτηση ορισμένη σ’ ένα
ανοικτό υποσύνολο 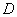 του
του 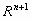 ,
τότε θα λέμε ότι η (2) είναι η κανονική
ή λυμένη της
μορφή.
,
τότε θα λέμε ότι η (2) είναι η κανονική
ή λυμένη της
μορφή.
Σημείωση:
H μορφή (1)
μιας Σ.Δ.Ε. θα λέγεται γενική ή
πεπλεγμένη.
Ορισμός 5
: Έστω ότι
δίνεται η διαφορική εξίσωση (2) και ένα
σημείο 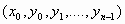 του
πεδίου ορισμού της
του
πεδίου ορισμού της 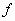 .
Το πρόβλημα της εύρεσης
μιας λύσης της (2) η οποία ικανοποιεί τις
συνθήκες
.
Το πρόβλημα της εύρεσης
μιας λύσης της (2) η οποία ικανοποιεί τις
συνθήκες

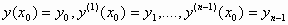 ,
(3)
,
(3)
λέγεται πρόβλημα αρχικών τιμών ή
πρόβλημα Cauchy για
την (2).
Οι συνθήκες (3) ονομάζονται αρχικές
συνθήκες ή συνθήκες Cauchy.
Ορισμός 6
: Μια
συνάρτηση
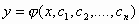 (4)
(4)
που εξαρτάται από
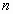 πραγματικές σταθερές
πραγματικές σταθερές 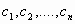 ,
θα λέγεται γενική
λύση της διαφορικής
εξίσωσης (2) όταν
,
θα λέγεται γενική
λύση της διαφορικής
εξίσωσης (2) όταν
(i) για κάθε σημείο
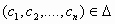 ,
όπου
,
όπου  ανοικτό υποσύνολο του
ανοικτό υποσύνολο του 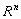 ,
η (1.4) είναι λύση της (2)
,
η (1.4) είναι λύση της (2)
και
(ii) για κάθε σημείο
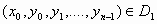 ,
όπου
,
όπου 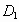 ανοικτό υποσύνολο του
πεδίου ορισμού
ανοικτό υποσύνολο του
πεδίου ορισμού 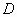 της
της 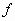 ,
υπάρχει ακριβώς ένα
σημείο
,
υπάρχει ακριβώς ένα
σημείο 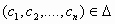 τέτοιο
ώστε η
τέτοιο
ώστε η 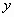 να
ικανοποιεί τις αρχικές συνθήκες (3).
να
ικανοποιεί τις αρχικές συνθήκες (3).
Η λύση που παίρνουμε για μια συγκεκριμένη
επιλογή των σταθερών 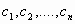 ,
ονομάζεται μερική λύση
της διαφορικής εξίσωσης (2).
,
ονομάζεται μερική λύση
της διαφορικής εξίσωσης (2).
Ορισμός 7
: Αν 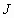 είναι ένα ανοικτό
υποδιάστημα του
είναι ένα ανοικτό
υποδιάστημα του 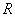 ,
θα λέμε ότι το σύστημα
,
θα λέμε ότι το σύστημα
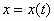 ,
, 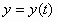 ,
,
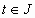
παράγει τη λύση
της
(2) υπό παραμετρική μορφή αν
και μόνον αν οι συναρτήσεις 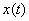 ,
,
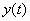 είναι
είναι
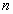 φορές
παραγωγίσιμες, η
φορές
παραγωγίσιμες, η 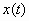 είναι αντιστρέψιμη και η
σύνθετη συνάρτηση
είναι αντιστρέψιμη και η
σύνθετη συνάρτηση
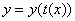
είναι λύση της (2).
Ορισμός 8
: Το
σύστημα των 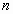 ισοτήτων
ισοτήτων
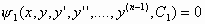 ,
,
…….……………………….. (5)
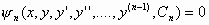 ,
,
θα λέμε ότι αποτελεί ένα γενικό
ολοκλήρωμα
της (2) όταν
για κάθε σημείο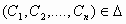 , όπου
, όπου
 ανοικτό
υποσύνολο του
ανοικτό
υποσύνολο του 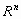 , υπάρχει
λύση
, υπάρχει
λύση 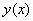 της
(2) η οποία ικανοποιεί τις σχέσεις (5) και,
αντίστροφα, όταν κάθε
της
(2) η οποία ικανοποιεί τις σχέσεις (5) και,
αντίστροφα, όταν κάθε 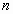 φορές παραγωγίσιμη
συνάρτηση
φορές παραγωγίσιμη
συνάρτηση 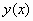 η
οποία ικανοποιεί τις (5) είναι λύση της (2).
η
οποία ικανοποιεί τις (5) είναι λύση της (2).
Παρατήρηση:
H διαδικασία
προσδιορισμού των λύσεων μιας διαφορικής εξίσωσης ονομάζεται επίλυση
ή ολοκλήρωση της
εξίσωσης.
[Επιστροφή
στα Περιεχόμενα]
![]() , (1)
, (1)![]() ,
,![]() .
.![]() , (2)
, (2)![]()
![]() ,
(3)
,
(3)![]() (4)
(4)![]() ,
, ![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,