Λύση
Η δοθείσα είναι εξίσωση
Bernoulli με
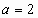 . Υποθέτοντας
ότι
. Υποθέτοντας
ότι 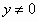 και
εκτελώντας το μετασχηματισμό Leibniz
και
εκτελώντας το μετασχηματισμό Leibniz
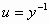 , (1)
, (1)
έχουμε
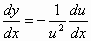
 ,
,
οπότε η εξίσωση γίνεται
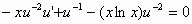 ,
,
ή
 . (2)
. (2)
Η (2) είναι γραμμική και έχει ως γενική λύση
την
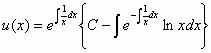
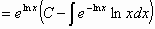
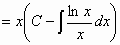
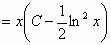 . (3)
. (3)
Ικανοποιώντας την αρχική συνθήκη, θέτουμε
στην (3)
 ,
, 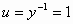 και παίρνουμε
και παίρνουμε 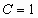 .
Έτσι, η λύση του δοθέντος
προβλήματος αρχικών τιμών δίνεται από τον
τύπο
.
Έτσι, η λύση του δοθέντος
προβλήματος αρχικών τιμών δίνεται από τον
τύπο
 . (4)
. (4)
Το πεδίο ορισμού της λύσης θα πρέπει
απαραίτητα να περιέχει το σημείο
 της αρχικής συνθήκης ενώ
παράλληλα να ισχύει
της αρχικής συνθήκης ενώ
παράλληλα να ισχύει 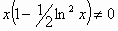 .
Έτσι, εύκολα προκύπτει ότι
το μέγιστο διάστημα ορισμού της λύσης είναι
το
.
Έτσι, εύκολα προκύπτει ότι
το μέγιστο διάστημα ορισμού της λύσης είναι
το 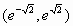 .
.
[Επιστροφή
στην Άσκηση 1]
![]() , (1)
, (1)![]()
![]() ,
,![]() ,
,![]() . (2)
. (2)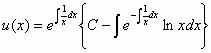
![]()
![]()
![]() . (3)
. (3) . (4)
. (4)