Λύση
Η διαφορική εξίσωση είναι γραμμική και
έχει ως ολοκληρώνοντα παράγοντα
τη
συνάρτηση
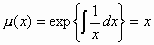 . (1)
. (1)
Έτσι, πολλαπλασιάζοντας αμφότερα τα μέλη
της
με 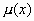 παίρνουμε
παίρνουμε
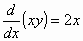 ,
,
και άρα
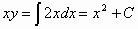 ,
,
ή
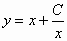 . (2)
. (2)
Για την ικανοποίηση της
αρχικής
συνθήκης θέτουμε
στην (2) 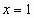 ,
, 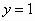 και παίρνουμε
και παίρνουμε 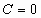 .
Συνεπώς, η
λύση του δοθέντος προβλήματος δίνεται
από τον τύπο
.
Συνεπώς, η
λύση του δοθέντος προβλήματος δίνεται
από τον τύπο
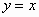 . (3)
. (3)
Αν και οι
συναρτήσεις 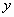 και
και 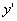 ορίζονται σε όλο το
ορίζονται σε όλο το 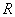 ,
το μέγιστο
διάστημα ορισμού της
λύσης του προβλήματος είναι
το
,
το μέγιστο
διάστημα ορισμού της
λύσης του προβλήματος είναι
το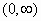 αφού
αυτό περιέχει το σημείο
αφού
αυτό περιέχει το σημείο 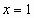 της αρχικής
συνθήκης ενώ παράλληλα ο συντελεστής
της αρχικής
συνθήκης ενώ παράλληλα ο συντελεστής 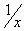 στη διαφορική
εξίσωση ορίζεται
παντού εκτός από το
στη διαφορική
εξίσωση ορίζεται
παντού εκτός από το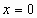 .
Αξίζει πάντως να σημειωθεί
ότι αν η διαφορική εξίσωση είχε δοθεί
αρχικά στη μορφή
.
Αξίζει πάντως να σημειωθεί
ότι αν η διαφορική εξίσωση είχε δοθεί
αρχικά στη μορφή
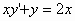
τότε το μέγιστο διάστημα ορισμού της
λύσης
του προβλήματος θα ήταν το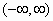 .
.
[Επιστροφή
στην Άσκηση 2]
![]() . (1)
. (1)![]() ,
,![]() ,
,![]() . (2)
. (2)![]() . (3)
. (3)![]()