Ορισμός: Μια διαφορική εξίσωση της μορφής

, (1)

όπου και είναι συνεχείς συναρτήσεις σ’ ένα διάστημα , λέγεται γραμμική διαφορική εξίσωση πρώτης τάξης.

Αν τότε η (1) λέγεται ομογενής γραμμική διαφορική εξίσωση πρώτης τάξης.

Η εξίσωση (1) έχει ως πολλαπλασιαστή Euler τη συνάρτηση

. (2)

Έτσι, πολλαπλασιάζοντας την (1) με , παίρνουμε

, (3)

και, ολοκληρώνοντας ως προς αμφότερα τα μέλη της (3), έχουμε

, (4)

όπου είναι μια αυθαίρετη πραγματική σταθερά. Ο τύπος (4) δίνει τη γενική λύση της γραμμικής εξίσωσης (1). Παρατηρούμε επιπλέον ότι λόγω της (2) είναι και συνεπώς δεν υπάρχουν ιδιάζουσες λύσεις. Στην περίπτωση που η (1) συνοδεύεται από την αρχική συνθήκη

, (5)

η λύση είναι μοναδική και δίνεται από την σχέση

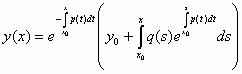. (6)

 [Επιστροφή στα Περιεχόμενα]

Να επιλυθούν τα προβλήματα αρχικών τιμών και να προσδιοριστεί το μέγιστο πεδίο ορισμού της λύσης:

1. , [Λύση]

2. , [Λύση]

3. Να λυθεί η διαφορική εξίσωση: [Υπόδειξη] , [Λύση]

4. Να λυθεί η διαφορική εξίσωση: [Υπόδειξη] , [Λύση]

[Επιστροφή στα Περιεχόμενα]