, (1)Λύση
Η δοθείσα διαφορική εξίσωση δεν είναι γραμμική.
Εναλλάσοντας όμως το ρόλο των μεταβλητών και θεωρώντας το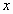
ως συνάρτηση του 
,
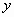προκύπτει ότι
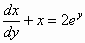, (1)
η οποία
είναι γραμμική εξίσωση ως προς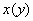
.
Έτσι, από την
(1) έχουμε
,
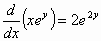οπότε
,
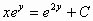ή
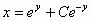, (2)
όπου
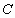είναι
μια αυθαίρετη πραγματική σταθερά. Η
σχέση (2) δίνει τη γενική
λύση της αρχικής διαφορικής
εξίσωσης σε πεπλεγμένη μορφή.