Έστω ένα κοινό σημείο καμπής των και στο . Παρατηρούμε ότι αφού οι και είναι λύσεις της δευτεροτάξιας γραμμικής εξίσωσης

, (1)

όπου οι συντελεστές και 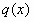είναι συνεχείς συναρτήσεις στο, θα έχουν συνεχείς δεύτερες παραγώγους στο και άρα στο σημείο καμπής θα είναι

. (2)

Συνεπώς από τις (1) και (2) θα έχουμε επίσης

, (3)

. (4)

Πολλαπλασιάζοντας τώρα την σχέση (3) με , την σχέση (4) με και αφαιρώντας κατά μέλη παίρνουμε ότι

,

, (5)

όπου είναι η τιμή της Wronskian των και στο σημείο . Αφού όμως αυτές είναι γραμμικώς ανεξάρτητες λύσεις της (1) στο , η δεν μηδενίζεται πουθενά στο και συνεπώς από την (5) προκύπτει ότι . Έτσι οι σχέσεις (3) και (4) παίρνουν τη μορφή

, (6)

, (7)

αντίστοιχα. Αν τώρα τότε θα πρέπει να είναι. Αυτό όμως είναι επίσης αδύνατο αφού . Άρα .

[Επιστροφή στην Άσκηση 7]