Έστω η ομογενής γραμμική διαφορική εξίσωση τάξης

, (1)

όπου οι συντελεστές , , είναι δοσμένες συνεχείς συναρτήσεις ορισμένες σ’ ένα ανοικτό διάστημα .

Ορισμός 1. Ορίζουμε τον διαφορικό τελεστή μέσω της σχέσης

, (2)

όπου , . Τότε η (1) γράφεται στη μορφή

. (3)

Άμεση συνέπεια του Ορισμού 1 είναι η ακόλουθες δύο προτάσεις:

Πρόταση 1. Ο τελεστής (2) είναι γραμμικός, δηλ.

,

για κάθε σταθερές , και κάθε -φορές διαφορίσιμες συναρτήσεις , .

Πρόταση 2. (Αρχή της υπέρθεσης λύσεων)

Αν , είναι δύο λύσεις της εξίσωσης (3) τότε και κάθε γραμμικός συνδυασμός τους , όπου , αυθαίρετες σταθερές, είναι επίσης λύση της (3).

Ορισμός 2. Θα λέμε ότι οι συναρτήσεις , οι οποίες ορίζονται σ’ ένα διάστημα , είναι γραμμικώς ανεξάρτητες (ή ότι το σύνολο είναι γραμμικώς ανεξάρτητο) αν οι μοναδικές σταθερές για τις οποίες ισχύει η ταυτότητα

, ,

είναι .

Θεώρημα 1. Κάθε ομογενής γραμμική διαφορική εξίσωση (3) έχει το πλήθος γραμμικώς ανεξάρτητες λύσεις. Αν είναι ένα τέτοιο σύνολο λύσεων τότε η γενική λύση της (3) δίνεται από την σχέση

, (4)

όπου είναι αυθαίρετες σταθερές.

Ορισμός 3. Έστω σύνολο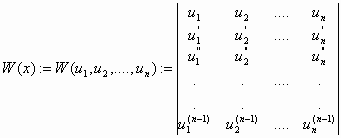 , το πλήθος συναρτήσεων οι οποίες ορίζονται σ’ ένα ανοικτό διάστημα και είναι -φορές συνεχώς παραγωγίσιμες σ’ αυτό. Η ορίζουσα

, (5)

ονομάζεται Wronkian του συνόλου .

Θεώρημα 2. (J. Liouville)

Αν είναι το πλήθος λύσεις της εξίσωσης (3) στο διάστημα , τότε για την ορίζουσα Wronski ισχύει ο ακόλουθος τύπος του Abel:

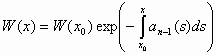, (6)

όπου .

Πόρισμα. Έστω ότι είναι το πλήθος λύσεις της εξίσωσης (3) στο διάστημα . Τότε, είτε

Ι) για κάθε ,

ΙΙ) στο .

Θεώρημα 3. Ένα σύνολο, το πλήθος λύσεων της εξίσωσης (3) είναι γραμμικώς ανεξάρτητο αν και μόνον αν η Wronskian στο .

Ορισμός 4. Κάθε σύνολο , το πλήθος λύσεων της εξίσωσης (3) στο διάστημα για το οποίο ισχύει ότι

στο ,

θα λέγεται θεμελιώδες σύνολο λύσεων της (3).

Σημείωση: Η ορίζουσα (5) ονομάζεται Wronskian προς τιμήν του Πολωνού μαθηματικού Joseph H. Wronski (1778 – 1853) που την εισήγαγε πρώτος. Ο τύπος (6) αποδείχθηκε το 1827 από τον Νορβηγό μαθηματικό Niels H. Abel (1802 – 1829) για και αργότερα γενικεύτηκε από τον Γάλλο μαθηματικό Joseph Liouville (1809 – 1882).

[Επιστροφή στα Περιεχόμενα] 

Εξετάστε αν οι παρακάτω συναρτήσεις είναι γραμμικώς ανεξάρτητες στο :

1. , [Λύση]

2. , , [Λύση]

3. Δείξτε ότι οι συναρτήσεις και είναι γραμμικώς ανεξάρτητες στο ενώ παράλληλα η Wronskian . [Λύση]

, ,

δέχεται ως λύσεις τις συναρτήσεις και οι οποίες είναι γραμμικώς ανεξάρτητες στο ενώ (βλέπε Άσκηση 3). Έρχεται αυτό σε αντίθεση με το Θεώρημα 3 ; [Λύση]

5. Δείξτε ότι συναρτήσεις και αποτελούν ένα θεμελιώδες σύνολο λύσεων της διαφορικής εξίσωσης

, . [Λύση]

6. Έστω , το πλήθος συναρτήσεις οι οποίες ορίζονται σ’ ένα ανοικτό διάστημα και είναι -φορές συνεχώς παραγωγίσιμες σ’ αυτό. Αν η Wronskian για κάθε , δείξτε ότι η διαφορική εξίσωση τάξης

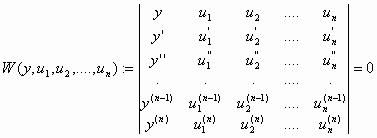
έχει ως θεμελιώδες σύνολο λύσεων τις συναρτήσεις .[Λύση]

7. Έστωκαι δύο γραμμικώς ανεξάρτητες λύσεις της διαφορικής εξίσωσης

,

όπου και είναι συνεχείς συναρτήσεις στο διάστημα . Δείξτε ότι οι συναρτήσεις και δεν μπορούν να έχουν κοινά σημεία καμπής στο εκτός αν οι συντελεστές και μηδενίζονται ταυτόχρονα σ’αυτά. [Λύση]

[Επιστροφή στα Περιεχόμενα]