Έστω η ομογενής γραμμική διαφορική εξίσωση τάξης

, (1)

όπου οι συντελεστές είναι δοθέντες πραγματικοί αριθμοί.

Ορισμός 1. Το πολυώνυμο

, (2)

, (3)

ονομάζονται χαρακτηριστικό πολυώνυμο και χαρακτηριστική εξίσωση, αντίστοιχα, της διαφορικής εξίσωσης (1).

Σημείωση: Το χαρακτηριστικό πολυώνυμο (2) παράγεται από το αριστερό μέλος της (1) αν αντικαταστήσουμε κάθε παράγωγο με .

Θεώρημα 1. Έστω ότι το χαρακτηριστικό πολυώνυμο (2) έχει τις διαφορετικές μεταξύ τους ρίζες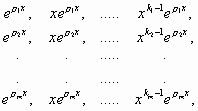 βαθμού πολλαπλότητας αντίστοιχα, όπου . Τότε η διαφορική εξίσωση (1) έχει τις γραμμικώς ανεξάρτητες λύσεις

(4)

, (5)

όπου είναι αυθαίρετες σταθερές.

Σημείωση: Αν μια ρίζα του χαρακτηριστικού πολύωνύμου είναι μιγαδική, έστω η (, ) με βαθμό πολλαπλότητας , τότε οι αντίστοιχες γραμμικώς ανεξάρτητες λύσεις της (1)

, (6)

δεν είναι πλέον πραγματικές συναρτήσεις. Εν τούτοις, με τη βοήθεια του γνωστού τύπου του Euler

,

μπορούμε να αντικαταστήσουμε τις μιγαδικές λύσεις (6) με τις πραγματικές λύσεις

,

(7)

.

Αξίζει να σημειωθεί εδώ ότι επειδή οι συντελεστές στην (1) είναι πραγματικοί αριθμοί, οι μιγαδικές ρίζες της (3), αν υπάρχουν, εμφανίζονται σε ζεύγη συζυγών, δηλ. . Έτσι, εύκολα προκύπτει ότι το σύνολο των πραγματικών λύσεων (7) αντιστοιχεί και στις δύο συζυγείς μιγαδικές ρίζες.

ΑΣΚΗΣΕΙΣ:

Να επιλυθούν οι διαφορικές εξισώσεις:

1. . [Λύση]

2. . [Λύση]

3. . [Λύση]

4. . [Λύση]

[Επιστροφή στα Περιεχόμενα]