

Next: Άσκηση
Up: Άσκηση
Previous: Υπόδειξη
Από την εξίσωση της περιφέρειας
xA + yB + C = - x2 - y2 αντικαθιστώντας
τις συντεταγμένες των τριών σημείων παίρνουμε το σύστημα
| 0A + 0B + C = 04A + 0B + C = - 163A - 5B + C = - 34 |
|
|
Λύνουμε το σύστημα και βρίσκουμε
A = - 4, B = 22/5 και C = 0, συνεπώς η εξίσωση
της περιγεγραμμένης περιφέρειας είναι
x2 +
y2 - 4
x +
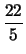 y
y = 0
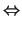
(
x - 2)
2 +
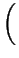 y
y +
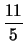
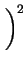
=
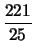
.
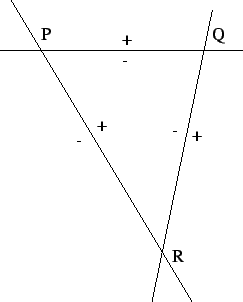
Οι πλευρές του τριγώνου δίνονται από τις ευθείες
(PQ) : 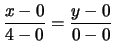 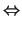 y = 0(PR) :
y = 0(PR) : 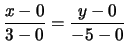 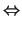 5x + 3y = 0(QR) :
5x + 3y = 0(QR) : 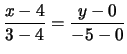  5x - y - 20 = 0
5x - y - 20 = 0 |
|
|
|
|
Στην εξίσωση της (PQ) αντικαταστήσουμε τις συντεταγμένες της κορυφής R
και βρίσκουμε -5 < 0, συνεπώς η κορυφή R βρίσκεται στο αρνητικό ημιεπίπεδο της
(PQ). Με παρόμοιο τρόπο βρίσκουμε ότι τι εσωτερικό του τριγώνου βρίσκεται στο
αρνητικό ημιεπίπεδο της (QR) και στο θετικό της (PR), όπως περιγράφεται
στο σχήμα.
Το κέντρο της εγγεγραμμένης περιφέρειας βρίσκεται στο εσωτερικό του τριγώνου
σε ίση απόσταση από όλες τις πλευρές του τριγώνου. Αν
K(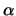 ,
,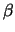 ) το
ζητούμενο κέντρο του εγγεγραμμένου κύκλου, τότε η απόσταση του απο τις πλευρές
του τριγώνου είναι ίση με την ακτίνα του κύκλου
) το
ζητούμενο κέντρο του εγγεγραμμένου κύκλου, τότε η απόσταση του απο τις πλευρές
του τριγώνου είναι ίση με την ακτίνα του κύκλου 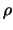 και έχουμε
και έχουμε
Λύνουμε τις εξισώσεις και βρίσκουμε
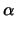
=
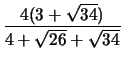
= 2, 36597 ,
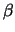
= -
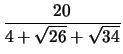
= - 1, 33959 ,
και
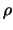 = -
= - 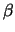 . Ο εγγεγραμμένος κύκλος είναι λοιπόν
. Ο εγγεγραμμένος κύκλος είναι λοιπόν
Aristophanes Dimakis
1999-10-05

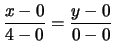
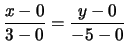
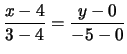
![]() ,
,![]() ) το
ζητούμενο κέντρο του εγγεγραμμένου κύκλου, τότε η απόσταση του απο τις πλευρές
του τριγώνου είναι ίση με την ακτίνα του κύκλου
) το
ζητούμενο κέντρο του εγγεγραμμένου κύκλου, τότε η απόσταση του απο τις πλευρές
του τριγώνου είναι ίση με την ακτίνα του κύκλου ![]() και έχουμε
και έχουμε
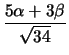 = -
= - 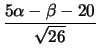 .
.
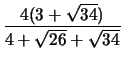 = 2, 36597 ,
= 2, 36597 , 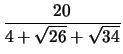 = - 1, 33959 ,
= - 1, 33959 ,