Λύση

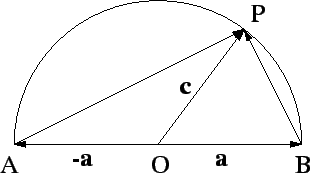
Έστω AB η διάμετρος της ημιπεριφέρειας, P ένα σημείο της, O το κέντρο και r η ακτίνα. Θέτουμε $\overrightarrow{OB}$ = $\vec{a}\,$ και $\overrightarrow{OP}$ = $\vec{c}\,$, οπότε $\overrightarrow{OA}$ = - $\vec{a}\,$. Από το σχήμα έχουμε $\overrightarrow{BP}$ = $\vec{c}\,$ - $\vec{a}\,$ και $\overrightarrow{AP}$ = $\vec{a}\,$ + $\vec{c}\,$ . Συνεπώς $\overrightarrow{AP}$ ^. $\overrightarrow{BP}$ = |$\vec{c}\,$|² - |$\vec{a}\,$|² = 0, διότι |$\vec{a}\,$| = |$\vec{c}\,$| = r. Άρα τα $\overrightarrow{AP}$,$\overrightarrow{BP}$ είναι κάθετα και η γωνία $\angle$APB είναι ορθή.