Λύση

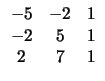
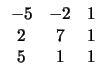
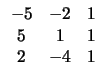
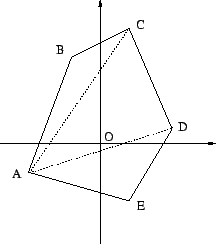
Αν φέρουμε τα ευθύγραμμα τμήματα AC και AD το πεντάγωνο χωρίζεται σε τρία τρίγωνα ABC, ACD και ADE. Το εμβαδον του πενταγώνου είναι το άθροισμα των εμβαδών των τριγώνων. Έχουμε λοιπόν

Εμβ(ABCDE)=Εμβ(ABC)+Εμβ(ACD)+Εμβ(ADE)=
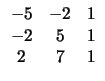
		$\displaystyle {1\over 2}$ \| $\displaystyle \left\vert\vphantom{\begin{array}{ccc} -5&-2&1\\ -2&5&1 \\ 2&7&1\end{array}}\right.$ $\displaystyle \begin{array}{ccc} -5&-2&1\\ -2&5&1 \\ 2&7&1\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{ccc} -5&-2&1\\ -2&5&1 \\ 2&7&1\end{array}}\right\vert$ \| + $\displaystyle {1\over 2}$ \| $\displaystyle \left\vert\vphantom{\begin{array}{ccc} -5&-2&1\\ 2&7&1\\ 5&1&1\end{array}}\right.$ $\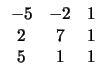displaystyle \begin{array}{ccc} -5&-2&1\\ 2&7&1\\ 5&1&1\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{ccc} -5&-2&1\\ 2&7&1\\ 5&1&1\end{array}}\right\vert$ \| + $\displaystyle {1\over 2}$ \| $\displaystyle \left\vert\vphantom{\begin{array}{ccc} -5&-2&1\\ 5&1&1\\ 2&-4&1\end{array}}\right.$ $\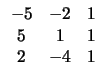displaystyle \begin{array}{ccc} -5&-2&1\\ 5&1&1\\ 2&-4&1\end{array}$ $\displaystyle \left.\vphantom{\begin{array}{ccc} -5&-2&1\\ 5&1&1\\ 2&-4&1\end{array}}\right\vert$ \|.