


Next: 'Ασκηση 2
Up: 'Ασκηση 1
Previous: Υπόδειξη
Λύση
Για 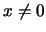 η συνάρτηση μας είναι συνεχής (γιατί;). Για να είναι συνεχής στο
η συνάρτηση μας είναι συνεχής (γιατί;). Για να είναι συνεχής στο 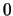 πρέπει
πρέπει
'Ομως
Άρα η συνάρτηση δεν είναι συνεχής στο 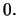 'Εχει μάλιστα
άρσιμη ασυνέχεια. Μπορούμε να αλλάξουμε την τιμή της στο 0 (να έχουμε
'Εχει μάλιστα
άρσιμη ασυνέχεια. Μπορούμε να αλλάξουμε την τιμή της στο 0 (να έχουμε 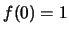 )
και να γίνει συνεχής σ' αυτό.
)
και να γίνει συνεχής σ' αυτό.
'Ασκηση 1
Υπόδειξη
Antonis Tsolomitis
1999-11-11