


Next: 'Ασκηση 7
Up: 'Ασκηση 6
Previous: Υπόδειξη
Λύση
'Εστω
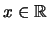 .
Επειδή το σύνολο των ρητών είναι πυκνό στο
.
Επειδή το σύνολο των ρητών είναι πυκνό στο 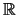 έχουμε
ότι υπάρχει ακολουθία
έχουμε
ότι υπάρχει ακολουθία 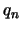 ρητών με
ρητών με
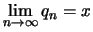 .
Αν στο
.
Αν στο 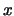 είναι
συνεχής πρέπει
είναι
συνεχής πρέπει
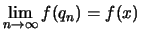 και άρα
και άρα 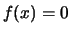 .
Επίσης, από την
πυκνότητα των αρρήτων στο
.
Επίσης, από την
πυκνότητα των αρρήτων στο 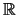 έχουμε ότι υπάρχει ακολουθία
έχουμε ότι υπάρχει ακολουθία 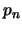 αρρήτων
με
αρρήτων
με
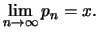 Αν στο
Αν στο 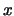 είναι συνεχής πρέπει
είναι συνεχής πρέπει
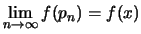 και άρα
και άρα 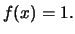 Από τα παραπάνω και σύμφωνα με γνωστό θεώρημα έχουμε
ότι η συνάρτηση δεν μπορεί να είναι συνεχής σε κανένα σημείο. 'Αρα είναι παντού
ασυνεχής. Mάλιστα έχει ουσιώδη ασυνέχεια (γιατί;).
Από τα παραπάνω και σύμφωνα με γνωστό θεώρημα έχουμε
ότι η συνάρτηση δεν μπορεί να είναι συνεχής σε κανένα σημείο. 'Αρα είναι παντού
ασυνεχής. Mάλιστα έχει ουσιώδη ασυνέχεια (γιατί;).
'Ασκηση 6
Υπόδειξη
Antonis Tsolomitis
1999-11-11