


Next: Υπόδειξη
Up: Ασκήσεις
Previous: Λύση
'Ασκηση 7
'Εστω συνεχής συνάρτηση
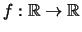 τέτοια ώστε
τέτοια ώστε
Αποδείξτε ότι:
(i) Η  είναι άνω φραγμένη.
είναι άνω φραγμένη.
(ii) Υπάρχει
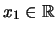 τέτοιο ώστε
τέτοιο ώστε
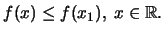
Υπάρχει
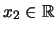 τέτοιο ώστε
τέτοιο ώστε
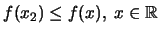 ;
Υπόδειξη
Λύση
;
Υπόδειξη
Λύση
Antonis Tsolomitis
1999-11-11
![]() είναι άνω φραγμένη.
είναι άνω φραγμένη.
![]() τέτοιο ώστε
τέτοιο ώστε
![]()
![]() τέτοιο ώστε
τέτοιο ώστε
![]() ;
Υπόδειξη
Λύση
;
Υπόδειξη
Λύση