


Next: Ομοιόμορφη συνέχεια
Up: 'Ασκηση 8
Previous: Υπόδειξη
Λύση
Αν 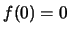 ή
ή 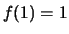 τότε το ζητούμενο σημείο θα είναι κάποιο από αυτά. 'Εστω δεν
συμβαίνει τίποτε από τα δύο αυτά. Τότε, λόγω της υπόθεσης θα έχουμε
τότε το ζητούμενο σημείο θα είναι κάποιο από αυτά. 'Εστω δεν
συμβαίνει τίποτε από τα δύο αυτά. Τότε, λόγω της υπόθεσης θα έχουμε 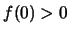 και
και
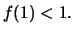 Θεωρούμε τη συνάρτηση
Θεωρούμε τη συνάρτηση
Η 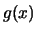 είναι συνεχής στο
είναι συνεχής στο ![$[0,1]$](img516.gif) αφού η
αφού η  και η ταυτοτική συνάρτηση είναι συνεχείς συναρτήσεις στο
και η ταυτοτική συνάρτηση είναι συνεχείς συναρτήσεις στο ![$[0,1]$](img516.gif) .
Επίσης
.
Επίσης
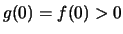 και
και
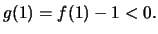 Άρα οι προ"υποθέσεις του θεωρήματος
της ενδιάμεσης τιμής ικανοποιούνται και άρα υπάρχει
Άρα οι προ"υποθέσεις του θεωρήματος
της ενδιάμεσης τιμής ικανοποιούνται και άρα υπάρχει
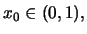 τέτοιο ώστε
τέτοιο ώστε 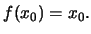 Συνδιάζοντας τα προηγούμενα έχουμε το ζητούμενο.
Συνδιάζοντας τα προηγούμενα έχουμε το ζητούμενο.
'Ασκηση 8
Υπόδειξη
Antonis Tsolomitis
1999-11-11