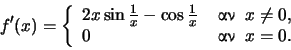Next: 'Ασκηση 3
Up: 'Ασκηση 2
Previous: Υπόδειξη
Λύση
Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο
 με
με
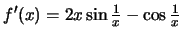 .
Εξετάζουμε την παραγωγισιμότητα στο
.
Εξετάζουμε την παραγωγισιμότητα στο 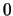 με τη
βοήθεια του ορισμού. 'Εχουμε
με τη
βοήθεια του ορισμού. 'Εχουμε
αφού
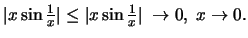 'Αρα η συνάρτηση είναι
παραγωγίσιμη και στο
'Αρα η συνάρτηση είναι
παραγωγίσιμη και στο 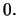 Τελικά έχουμε
Τελικά έχουμε
Από τη σχέση αυτή έχουμε ότι η 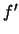 είναι συνεχής για
είναι συνεχής για
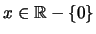 .
Στο
.
Στο 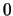 η
η
 δεν είναι συνεχής αφού δεν υπάρχει το όριο
δεν είναι συνεχής αφού δεν υπάρχει το όριο
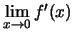 όπως
μπορεί να διαπιστώσει κανείς με τρόπο ανάλογο της άσκησηs 6.
όπως
μπορεί να διαπιστώσει κανείς με τρόπο ανάλογο της άσκησηs 6.
'Ασκηση 2
Υπόδειξη
Antonis Tsolomitis
1999-11-11