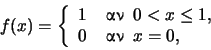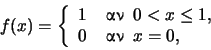Next: 'Ασκηση 12
Up: 'Ασκηση 11
Previous: Υπόδειξη
Λύση
Θα πρέπει απαραίτητα η συνάρτηση που θα κατασκευάσουμε να είναι ασυνεχής σε
ένα τουλάχιστο από τα σημεία 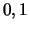 (δεν είναι ικανό αυτό).
'Εστω
(δεν είναι ικανό αυτό).
'Εστω
τότε
Αν
ίσχυε το θεώρημα μέσης τιμής, θα έπρεπε να υπάρχει
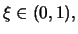 τέτοιο ώστε
τέτοιο ώστε
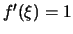 .
'Ομως για κάθε
.
'Ομως για κάθε 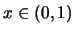 έχουμε
έχουμε 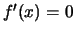 .
Άρα η
.
Άρα η  είναι ένα παράδειγμα
μιας συνάρτησης
είναι ένα παράδειγμα
μιας συνάρτησης
![$f : [0,1] \rightarrow \mathbb R$](img691.gif) ,
παραγωγίσιμης στο
,
παραγωγίσιμης στο 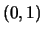 (σταθερή στο
(σταθερή στο 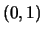 ),
για την οποία δεν ισχύει το συμπέρασμα του θεωρήματος της μέσης τιμής.
),
για την οποία δεν ισχύει το συμπέρασμα του θεωρήματος της μέσης τιμής.
'Ασκηση 11
Υπόδειξη
Antonis Tsolomitis
1999-11-11