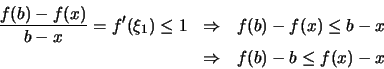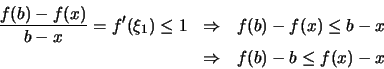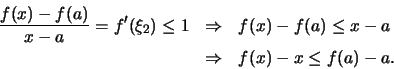Next: 'Ασκηση 13
Up: 'Ασκηση 12
Previous: Υπόδειξη
Λύση
Αν 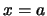 ή
ή 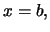 τότε προφανώς ισχύει η ισότητα. 'Εστω
τότε προφανώς ισχύει η ισότητα. 'Εστω 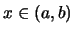 .
Επειδή η
.
Επειδή η  είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο ![$[α, b],$](img735.gif) μπορούμε να εφαρμόσουμε το θεώρημα
μέσης τιμής στα διαστήματα
μπορούμε να εφαρμόσουμε το θεώρημα
μέσης τιμής στα διαστήματα ![$[a,x]$](img743.gif) και
και ![$[x,b]$](img744.gif) .
'Εχουμε
.
'Εχουμε
και
Λόγω της υπόθεσης έχουμε
και άρα από τις παραπάνω ανισότητες έχουμε
'Ασκηση 12
Υπόδειξη
Antonis Tsolomitis
1999-11-11