Λύση

Από τη σχέση 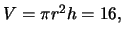$V = \pi r^2h = 16,$ έχουμε 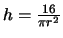$h = \frac{16}{\pi r^2}$ και άρα

$$Ε = Ε(r) = 2\pi r h + 2\pi r^2 = \frac{32\pi r}{\pi r^2} + 2\pi r^2 = \frac{32}{r} + 2\pi r^2.$$

Παραγωγίζοντας έχουμε

$$Ε'(r) = - \frac{32}{r^2} + 4\pi r.$$

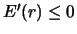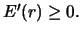Παρατηρούμε ότι για $0 < r \leq \frac{2}{\sqrt[3] \pi}$ είναι $E'(r) \leq 0$ και για $r \geq \frac{2}{\sqrt[3] \pi}$ είναι $E'(r) \geq 0.$ Από τα κριτήρια μονοτονίας, έχουμε ότι στο διάστημα $[0, \frac{2}{\sqrt[3] \pi}]$ η συνάρτηση είναι φθίνουσα ενώ στο διάστημα $[\frac{2}{\sqrt[3] \pi}, +\infty)$ η συνάρτηση είναι αύξουσα. ’ρα το εμβαδόν της παράπλευρης επιφάνειας γίνεται ελάχιστο για

$$r = \frac{2}{\sqrt[3] \pi}\;\; \hbox{και άρα} \;\; h = \frac{4}{\sqrt[3] \pi}.$$

'Ασκηση 19 Υπόδειξη