


Next: Ακολουθίες πραγματικών αριθμών
Up: 'Ασκηση 6
Previous: Υπόδειξη
Λύση
Επειδή τα 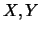 είναι μη κενά και άνω φραγμένα υποσύνολα του
είναι μη κενά και άνω φραγμένα υποσύνολα του 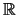 ,
σύμφωνα με το αξίωμα της πληρότητας, έχουμε ότι υπάρχουν οι αριθμοί
,
σύμφωνα με το αξίωμα της πληρότητας, έχουμε ότι υπάρχουν οι αριθμοί
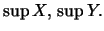 Χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι
Χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι
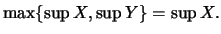 'Εστω
'Εστω
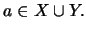 Τότε αν
Τότε αν 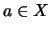 θα είναι
θα είναι 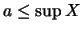 και αν
και αν 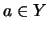 θα είναι
θα είναι
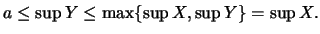 'Αρα ο αριθμός
'Αρα ο αριθμός 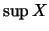 είναι
ένα άνω φράγμα του
είναι
ένα άνω φράγμα του 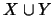 ,
το οποίο είναι μη κενό αφού τα
,
το οποίο είναι μη κενό αφού τα 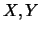 είναι μη κενά.
Σύμφωνα με το αξίωμα της πληρότητας θα έχει ελάχιστο άνω φράγμα,
είναι μη κενά.
Σύμφωνα με το αξίωμα της πληρότητας θα έχει ελάχιστο άνω φράγμα,
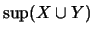 ,
το οποίο θα δείξουμε ότι είναι ίσο με
,
το οποίο θα δείξουμε ότι είναι ίσο με 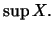 Είδαμε ότι ο αριθμός
Είδαμε ότι ο αριθμός 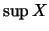 αποτελεί
άνω φράγμα του
αποτελεί
άνω φράγμα του 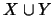 και άρα από το αξίωμα της πληρότητας θα έχουμε
και άρα από το αξίωμα της πληρότητας θα έχουμε
Για να έχουμε τη ζητούμενη ανισότητα αρκεί να δείξουμε ότι
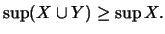 'Εστω
'Εστω 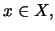 τότε
τότε
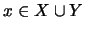 και
και
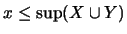 δηλαδή ο αριθμός
δηλαδή ο αριθμός
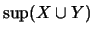 είναι άνω φράγμα του συνόλου
είναι άνω φράγμα του συνόλου 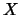 και άρα
και άρα
Από τα
παραπάνω έχουμε το ζητούμενο.
'Ασκηση 6
Υπόδειξη
Antonis Tsolomitis
1999-11-11