Next: 'Ασκηση 22
Up: 'Ασκηση 21
Previous: Υπόδειξη
Λύση
Θεωρούμε τη συνάρτηση
Έχουμε
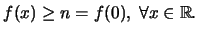 Δηλαδή το
Δηλαδή το 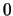 είναι ολικό και τοπικό
ελάχιστο. Επειδή η
είναι ολικό και τοπικό
ελάχιστο. Επειδή η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με
θα πρέπει σύμφωνα με το Θεώρημα του
Fermat, 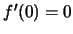 δηλαδή
δηλαδή
'Ασκηση 21
Υπόδειξη
Antonis Tsolomitis
1999-11-11