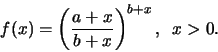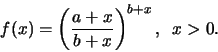Next: 'Ασκηση 23
Up: 'Ασκηση 22
Previous: Υπόδειξη
Λύση
Θεωρούμε τη συνάρτηση
Είναι
Για να βρούμε τη μονοτονία της  ,
αρκεί να ελέγξουμε το πρόσημο της
,
αρκεί να ελέγξουμε το πρόσημο της
(είναι
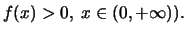 'Εχουμε
'Εχουμε
Άρα η 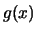 είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο 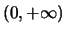 ,
οπότε (γιατί ;)
,
οπότε (γιατί ;)
Επειδή
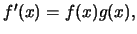 έχουμε
ότι
έχουμε
ότι 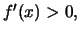 δηλαδή η
δηλαδή η 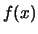 είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο 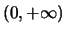 και άρα
και άρα
'Ασκηση 22
Υπόδειξη
Antonis Tsolomitis
1999-11-11