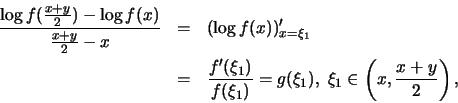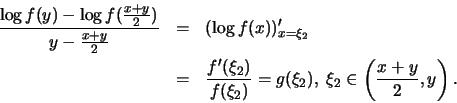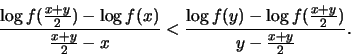Next: 'Ασκηση 24
Up: 'Ασκηση 23
Previous: Υπόδειξη
Λύση
Επειδή
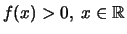 μπορούμε να ορίσουμε τη συνάρτηση
μπορούμε να ορίσουμε τη συνάρτηση
Επειδή η  είναι δύο φορές παραγωγίσιμη, έχουμε
ότι η
είναι δύο φορές παραγωγίσιμη, έχουμε
ότι η  και η
και η 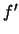 είναι παραγωγίσιμες και κατά συνέπεια και η
είναι παραγωγίσιμες και κατά συνέπεια και η 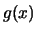 .
Είναι
.
Είναι
και άρα λόγω της υπόθεσης
![$f''(x)f(x) - [f'(x)]^2 > 0, \; x\in \mathbb R,$](img864.gif) έχουμε ότι
έχουμε ότι 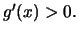 Σύμφωνα με γνωστό
θεώρημα η
Σύμφωνα με γνωστό
θεώρημα η 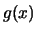 είναι γνήσια αύξουσα.
είναι γνήσια αύξουσα.
Στη συνέχεια θα δείξουμε την ανισότητα:
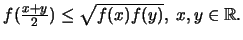
1oς τρόπος. Χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι 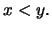 Θέτοντας
Θέτοντας
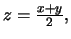 έχουμε
έχουμε 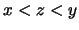 και αρκεί να δείξουμε την ανισότητα
και αρκεί να δείξουμε την ανισότητα
(γιατί;) ή ισοδύναμα, λόγω της
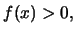 την
την
Θεωρούμε
την συνάρτηση
Είναι
αφού 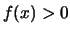 και όπως έχουμε δει η
και όπως έχουμε δει η 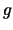 είναι γνήσια αύξουσα ενώ
είναι γνήσια αύξουσα ενώ 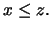 'Αρα η
'Αρα η
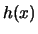 είναι γνήσια φθίνουσα, οπότε
είναι γνήσια φθίνουσα, οπότε
σχέση που δίνει την ζητούμενη
ανισότητα.
2os τρόπος. Επειδή
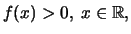 μπορούμε να ορίσουμε τη συνάρτηση
μπορούμε να ορίσουμε τη συνάρτηση
(υποθέτουμε ότι 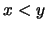 ). Η
). Η 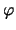 είναι συνεχής
και παραγωγίσιμη στο
είναι συνεχής
και παραγωγίσιμη στο ![$[x, y]$](img716.gif) ,
οπότε μπορούμε να εφαρμόσουμε το θεώρημα μέσης
τιμής στα διαστήματα
,
οπότε μπορούμε να εφαρμόσουμε το θεώρημα μέσης
τιμής στα διαστήματα
![$[x, \frac{x+y}{2}]$](img880.gif) ,
,
![$[\frac{x+y}{2}, y]$](img881.gif) και έχουμε:
και έχουμε:
Επειδή η 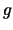 είναι γνήσια
αύξουσα και
είναι γνήσια
αύξουσα και
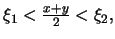 έχουμε ότι
έχουμε ότι
Κάνoντας τις σχετικές απλοποιήσεις καταλήγουμε στη ζητούμενη ανισότητα.
'Ασκηση 23
Υπόδειξη
Antonis Tsolomitis
1999-11-11
![]()
![]() Θέτοντας
Θέτοντας
![]() έχουμε
έχουμε ![]() και αρκεί να δείξουμε την ανισότητα
και αρκεί να δείξουμε την ανισότητα
![\begin{eqnarray*}
h'(x) &=& f'(x)f(2z - x) - f(x)f'(2z - x) \\ &= &\frac{1}{f(x)...
...{1}{f(x)f(2z - x)} [g(x) - g(2z -x)] < 0, \; x \in (-\infty, z],
\end{eqnarray*}](img873.gif)
![]() μπορούμε να ορίσουμε τη συνάρτηση
μπορούμε να ορίσουμε τη συνάρτηση