


Next: 'Ασκηση 25
Up: 'Ασκηση 24
Previous: Υπόδειξη
Λύση
 Είναι
Είναι
και
λόγω της υπόθεσης. 'Αρα η συνάρτηση είναι κυρτή λόγω γνωστού θεωρήματος.
 Από τη σχέση
Από τη σχέση 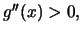 έχουμε ότι η
έχουμε ότι η 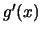 είναι γνήσια αύξουσα, οπότε αν
είναι γνήσια αύξουσα, οπότε αν
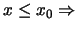
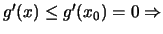 η
η 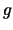 φθίνουσα στο
φθίνουσα στο
![$(-\infty, x_0] \Rightarrow$](img897.gif)
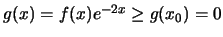
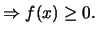 Το ίδιο συμπέρασμα έχουμε και για
Το ίδιο συμπέρασμα έχουμε και για 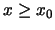 .
.
'Ασκηση 24
Υπόδειξη
Antonis Tsolomitis
1999-11-11
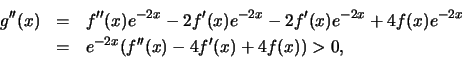
![]() Από τη σχέση
Από τη σχέση ![]() έχουμε ότι η
έχουμε ότι η ![]() είναι γνήσια αύξουσα, οπότε αν
είναι γνήσια αύξουσα, οπότε αν
![]()
![]() η
η ![]() φθίνουσα στο
φθίνουσα στο
![]()
![]()
![]() Το ίδιο συμπέρασμα έχουμε και για
Το ίδιο συμπέρασμα έχουμε και για ![]() .
.