


Next: 'Ασκηση 30
Up: 'Ασκηση 29
Previous: Υπόδειξη
Λύση
Στον υπολογισμό του ορίου με βάση της ιδιότητες εμφανίζονται απροσδιόριστες μορφές
γι' αυτό το μετασχηματίζουμε κατάλληλα ώστε να μπορέσουμε να εφαρμόσουμε τον
κανόνα του L' Hospital. Είναι
με
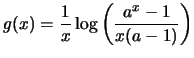 .
Αρκεί να
βρούμε το
.
Αρκεί να
βρούμε το
 Στο όριο αυτό εμφανίζεται απροσδιοριστία
της μορφής
Στο όριο αυτό εμφανίζεται απροσδιοριστία
της μορφής
 (γιατί;). Έχουμε
(γιατί;). Έχουμε
Παίρνοντας όρια στην παραπάνω ισότητα έχουμε το ζητούμενο αποτέλεσμα.
'Ασκηση 29
Υπόδειξη
Antonis Tsolomitis
1999-11-11
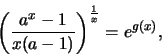
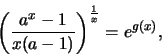
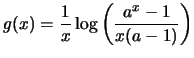 .
Αρκεί να
βρούμε το
.
Αρκεί να
βρούμε το
![\begin{displaymath}\frac{\left[\log \left({{a^x -1}\over {x(a-1)}}\right)\right]...
...a<1,$\cr\;
\frac{a^x}{a^x-1} \log a - \frac{1}{x} \;&$1<a$.\cr}\end{displaymath}](img934.gif)