


Next: 'Ασκηση 5
Up: 'Ασκηση 4
Previous: Υπόδειξη
Λύση
Έστω
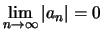 .
Από τον ορισμό της σύγκλισης έχουμε ότι για κάθε
.
Από τον ορισμό της σύγκλισης έχουμε ότι για κάθε
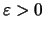 υπάρχει
υπάρχει
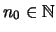 τέτοιο ώστε, για κάθε φυσικό
τέτοιο ώστε, για κάθε φυσικό 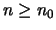 να έχουμε
να έχουμε
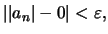 δηλαδή
δηλαδή
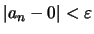 .
Αυτό όμως, πάλι
σύμφωνα με τον ορισμό της σύγκλισης, σημαίνει ότι
.
Αυτό όμως, πάλι
σύμφωνα με τον ορισμό της σύγκλισης, σημαίνει ότι
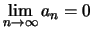 .
.
'Ασκηση 4
Υπόδειξη
Antonis Tsolomitis
1999-11-11