


Next: 'Ασκηση 13
Up: 'Ασκηση 12
Previous: Υπόδειξη
Λύση
Έστω
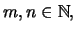 με
με 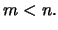 'Εχουμε
'Εχουμε
Επειδή 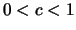 έχουμε ότι η ακολοθία
έχουμε ότι η ακολοθία
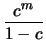 είναι μηδενική. 'Εστω
είναι μηδενική. 'Εστω
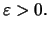 Υπάρχει
Υπάρχει
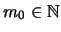 τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε 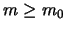 να
έχουμε
να
έχουμε
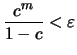 και άρα
και άρα
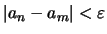 για
για
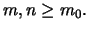 Άρα η ακολουθία είναι Cauchy και σύμφωνα με γνωστό θεώρημα
συγκλίνει.
Άρα η ακολουθία είναι Cauchy και σύμφωνα με γνωστό θεώρημα
συγκλίνει.
'Ασκηση 12
Υπόδειξη
Antonis Tsolomitis
1999-11-11
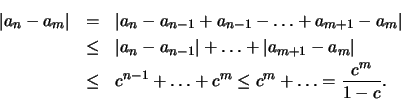
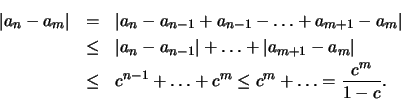
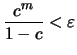 και άρα
και άρα