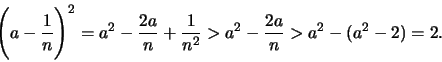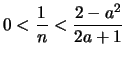 και άρα
και άρα
(i) Έστω ![]() Θα δείξουμε ότι υπάρχει
Θα δείξουμε ότι υπάρχει
![]() ,
τέτοιο ώστε
,
τέτοιο ώστε
![]() ,
γεγονός που έρχεται σε αντίθεση με την υπόθεση ότι
,
γεγονός που έρχεται σε αντίθεση με την υπόθεση ότι ![]() Πράγματι από την Αρχιμήδεια ιδιότητα των πραγματικών αριθμών έχουμε ότι
υπάρχει
Πράγματι από την Αρχιμήδεια ιδιότητα των πραγματικών αριθμών έχουμε ότι
υπάρχει
![]() τέτοιο ώστε
τέτοιο ώστε
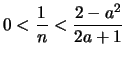 και άρα
και άρα
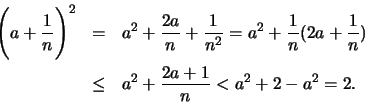
(ii) Έστω ![]() Θα δείξουμε ότι υπάρχει
Θα δείξουμε ότι υπάρχει
![]() τέτοιο ώστε
τέτοιο ώστε
![]() ,
γεγονός που έρχεται σε αντίθεση με την υπόθεση ότι
,
γεγονός που έρχεται σε αντίθεση με την υπόθεση ότι ![]() Πράγματι από την Αρχιμήδεια ιδιότητα των πραγματικών αριθμών έχουμε ότι υπάρχει
Πράγματι από την Αρχιμήδεια ιδιότητα των πραγματικών αριθμών έχουμε ότι υπάρχει
![]() τέτοιο ώστε
τέτοιο ώστε
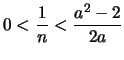 και άρα
και άρα