Λύση

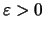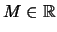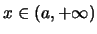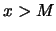Σύμφωνα με τον ορισμό του ορίου έχουμε ότι για κάθε $\varepsilon >0$ υπάρχει $Μ \in \mathbb R$ τέτοιο ώστε για κάθε $x \in (a, +\infty)$ με $x > M$ να έχουμε 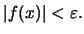$\vert f(x)\vert < \varepsilon.$ Δηλαδή

$$- \varepsilon < f(x) < \varepsilon\;\; \hbox{για}\;\; x > \max(a, M).$$

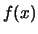Επειδή η $f(x)$ είναι φθίνουσα θα έχουμε και ότι

$$- \varepsilon < f(x) \;\; \hbox{για} \;\; a < x \leq \max(a, M)$$

και άρα

$$- \varepsilon < f(x) \;\; \hbox{για} \;\; a < x.$$

Επειδή το 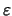$\varepsilon$ είναι τυχαίος θετικός αριθμός, έχουμε το ζητούμενο.

'Ασκηση 5 Υπόδειξη