Oρισμός: Έστω Χ=(x₁,…,x_n), Y=(y₁,…,y_n) δύο στοιχεία του Rⁿ. Tο εσωτερικό τους γινόμενο Χ· Υ είναι ο πραγματικός αριθμός x₁ y_1+…+ x_n y_n.

1. Χ· Υ=Υ· Χ
2. Ζ· (Χ+Υ)=Ζ· Χ+Ζ· Υ
3. (αΧ)· Υ=α(Χ· Υ) για κάθε αR.
4. Χ· Χ>0 « Χ0

Αν Χ· Υ=0 τα Χ,Υ θα λέγονται κάθετα.

Ορισμός: Έστω Χ=(x₁,…,x_n) Rⁿ. Η νόρμα του Χ είναι ο μη αρνητικός αριθμός

Η νόρμα του Χ μας δίνει την απόσταση του Χ από την αρχή των αξόνων (κάντε ένα σχήμα στο R² και μετά στο R³).

Έστω r>0 και Α Rⁿ. To σύνολο

λέγεται ανοικτή μπάλα με κέντρο Α και ακτίνα r, το δε σύνολο

λέγεται κλειστή μπάλα με κέντρο Α και ακτίνα r.

Το σύνολο

λέγεται σφαίρα με κέντρο Α και ακτίνα r.

Τα στοιχεία του συνόλου S(0,1) λέγονται μοναδιαία. Παρατηρούμε ότι αν Α0, το

Έστω Χ,ΥRⁿ με Χ· Υ=0. Τότε

 Έστω Χ, ΥRⁿ με Υ0. Το διάνυσμα

 λέγεται προβολή του Χ επί του Υ.

Για κάθε Χ,ΥRⁿ ισχύει

Ο μοναδικός πραγματικός θ[0,π] που ικανοποιεί την ισότητα

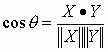
λέγεται γωνία μεταξύ των Χ,Υ.                                         [Επιστροφή στο κεφ. 11]

2. Nα υπολογίσετε την γωνία των διανυσμάτων Χ=(1,1) και Υ=(1,0). [Λύση]

3. Έστω Χ,ΥRⁿ. Να αποδειχθεί ότι

                     [Λύση]

4.Υποθέτουμε ότι μια δύναμη που δίνεται από το διάνυσμα (2,2) ασκείται σε ένα αντικείμενο που κινείται στην κατεύθυνση (2,1). Να εκφράσετε αυτή την δύναμη σαν άθροισμα μιας δύναμης που έχει την κατεύθυνση της κίνησης και μιας δύναμης που είναι κάθετη στην κατεύθυνση της κίνησης. [Υπόδειξη] [Λύση] 

[Περιεχόμενα]